Cálculo de volúmenes por integración directa

En este apartado introduciremos el método más general para el cálculo de volúmenes en el espacio. Del mismo modo que hacíamos en el caso de superficies en el plano, el método para calcular volúmenes es integrar la función $1$ (integral en sentido de $R^{3}$ , o sea, integral triple) en el dominio determinado, en este caso nuestro volumen.

Por lo tanto, otra vez la dificultad se encuentra en como parametrizar este volumen, más que como integrar.

Si queremos conocer el volumen de la región $V$ , tendremos:

$Vol (V) = ∭_{V} 1 d x d y d z$

Del mismo modo que en integrales dobles, a veces nos es más fácil hacer un cambio de coordenadas. En tal caso, tendremos que multiplicar por el determinante de la matriz Jacobiana. A continuación presentamos los cambios (y sus determinantes) más típicos en el cálculo de volúmenes, las esféricas y las cilíndricas:

Esféricas

$\begin{array}{l} x = r \cdot \sin θ \cdot \cos φ \\ y = r \cdot \sin θ \cdot \sin φ \\ z = r \cdot \cos θ \end{array} con det = r^{2} \sin θ$
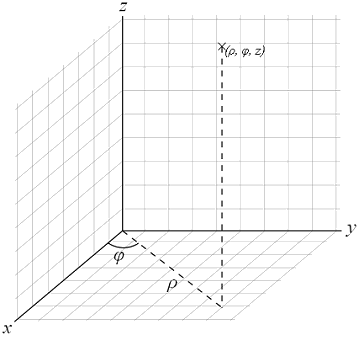
Cilíndricas

$\begin{array}{l} x = r \cdot \cos φ \\ y = r \cdot \sin φ \\ z = z \end{array} con det = r$

Ejemplo

Vamos a calcular el volumen delimitado por el paraboloide de ecuación $x^{2} + y^{2} = z$ y el plano $z = 1$ .

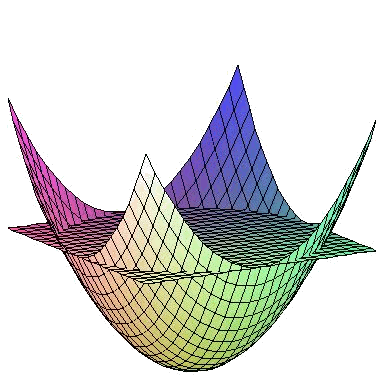
imagen

Por la simetría del problema consideraremos coordenadas cilíndricas. Tenemos:

$\begin{array}{l} x = r \cdot \cos φ \\ y = r \cdot \sin φ \\ z = z \end{array} con \begin{array}{l} r \in [0, \sqrt{z}] \\ θ \in [0, 2 π] \\ z \in [0, 1] \end{array}$

Teninedo en cuenta que el determinante del cambio es $r$ , tenemos:

$\begin{aligned} Vol = & ∭_{V} 1 d x d y d z = \int_{0}^{1} \int_{0}^{2 π} \int_{0}^{\sqrt{z}} r d r d θ d z = \int_{0}^{1} \int_{0}^{2 π} [\frac{r^{2}}{2}]_{0}^{\sqrt{z}} d θ d z \\ = & \int_{0}^{1} \int_{0}^{2 π} \frac{z}{2} d θ d z = \int_{0}^{1} π \cdot z d z = π [\frac{z^{2}}{2}]_{0}^{1} = \frac{π}{2} \end{aligned}$