Cálculo de volúmenes a partir del teorema de Gauss

De la misma forma que se hace con el teorema de Green, utilizaremos una potente herramienta del cálculo integral para calcular volúmenes, el teorema de la divergencia o teorema de Gauss.

Este teorema nos dice que si tenemos un sólido $D$ limitado por una superficie cerrada $S$ y $\vec{F} (x, y, z)$ un campo vectorial, entonces:

$\int_{S} \vec{F} d \vec{S} = ∭_{V} div (\vec{F}) d x d y d z$

donde, si $\vec{F} (x, y, z) = (P (x, y, z), Q (x, y, z), R (x, y, z))$ , entonces $div (\vec{F}) = P_{x} + Q_{y} + R_{z}$ es la divergencia del campo.

Recordamos que para calcular el primer término, si $r (u, v)$ ées una parametrización de la superficie,

$\int_{S} \vec{F} d \vec{S} = \iint \vec{F} (r (u, v)) \cdot (r_{u} \times r_{v}) d u d v$

donde $r_{u} \times r_{v}$ denota el producto vectorial de las derivadas de la parametrización según $u$ y $v$ .

Por lo tanto, si encontramos un campo que tenga divergencia idénticamente igual a $1$ , en el miembro de la derecha tendremos el volumen del sólido y por lo tanto tenemos un método para calcular volúmenes.

De campos que cumplan lo que necesitamos hay muchos, pero los más típicos son:

$\vec{F} (x, y, z) = (x, 0, 0)$
$\vec{F} (x, y, z) = (0, y, 0)$
$\vec{F} (x, y, z) = (0, 0, z)$
$\vec{F} (x, y, z) = \frac{1}{3} (x, y, z)$

Ejemplo

Vamos a calcular el volumen delimitado por media esfera y el plano ecuatorial, es decir:

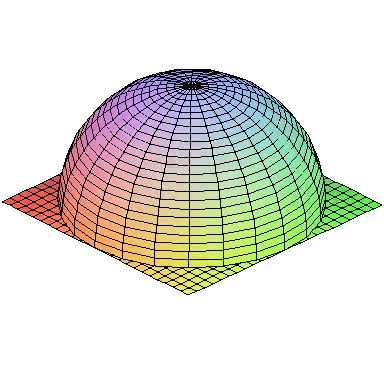
imagen

Por el teorema de Gauss tenemos que podemos integrar uno de los campos dado a lo largo de la superficie que encierra el volumen.

Parametricemos primero el casquete con coordenadas esféricas:

$\begin{array}{l} x = \sin θ \cos φ \\ y = \sin θ \sin φ \\ z = \cos θ \end{array} \begin{array}{l} θ \in [0, \frac{π}{2}] \\ φ \in [0, 2 π] \end{array}$

Calculemos los vectores derivadas y su producto vectorial:

$\begin{array}{l} r_{θ} = (\cos θ \cos φ, \sin φ \cos θ, - \sin φ) \\ r_{φ} = (- \sin θ \sin φ, \sin θ \cos φ, 0) \end{array}} \Rightarrow$

$\begin{aligned} \Rightarrow r_{θ} \times r_{φ} = & | \begin{array}{c} i & j & k \\ \cos θ \cos φ & \sin φ \cos θ & - \sin φ \\ - \sin θ \sin φ & \sin θ \cos φ & 0 \end{array} | \\ = & (\sin^{2} θ \cos φ, \sin^{2} θ \sin φ, \sin θ \cos θ) \end{aligned}$

Tomando el campo vecotorial $F (x, y, z) = (0, 0, z)$ , tenemos:

$\begin{aligned} \int_{S} (0, 0, z) d \vec{S} = & \int_{0}^{\frac{π}{2}} \int_{0}^{2 π} (0, 0, \cos θ) \cdot (\sin^{2} θ \cos φ, \sin^{2} θ \sin φ, \sin θ \cos θ) d φ d θ \\ = & \int_{0}^{\frac{π}{2}} \int_{0}^{2 π} \cos^{2} θ \cdot \sin θ d φ d θ = \int_{0}^{\frac{π}{2}} \cos^{2} θ \cdot \sin θ (\int_{0}^{2 π} d φ) d θ \\ = & 2 π \int_{0}^{\frac{π}{2}} \cos^{2} θ \cdot \sin θ d θ = 2 π [\frac{- \cos^{3} θ}{3}]_{0}^{\frac{π}{2}} = \frac{2}{3} π \end{aligned}$

Ahora debemos integrar el mismo campo sobre el la tapa inferior ya que el teorema es válido por superficies cerradas. Una parametrización del círculo es:

$\begin{array}{l} x = r \cos (t) \\ y = r \sin (t) \\ z = 0 \end{array} \begin{array}{l} t \in [0, 2 π] \\ r \in [0, 1] \end{array}$

Calculemos también los vectores derivadas y su producto vectorial:

$\begin{array}{l} r_{r} = (- r \sin (t), r \cos (t), 0) \\ r_{t} = (\cos (t), \sin (t), 0) \end{array}} \Rightarrow$

$\Rightarrow r_{t} \times r_{r} = | \begin{matrix} i & j & k \\ - r \sin (t) & r \cos (t) & 0 \\ \cos (t) & \sin (t) & 0 \end{matrix} | = (0, 0, - r^{2})$

Ahora, tenemos:

$\int_{C} (0, 0, z) d \vec{S} = \int_{0}^{2 π} \int_{0}^{1} (0, 0, 0) \cdot (0, 0, - r^{2}) d r d t = 0$

Por lo tanto,

$\begin{aligned} Vol (E) = & ∭_{S} 1 d x d y d z = ∭_{E} div (0, 0, z) d x d y d z \\ = & \int_{S} (0, 0, z) d \vec{S} + \int_{C} (0, 0, z) d \vec{S} = \frac{2}{3} π + 0 = \frac{2}{3} π \end{aligned}$