La moda de un conjunto de datos es el valor que aparece con una mayor frecuencia.
Se tira un dado diez veces y los resultados son los siguientes:
$$$1, 3, 2, 5, 4, 2, 6, 2, 3, 6$$$
Se observa la tabla de frecuencias absolutas:
| Resultado del dado | Frecuencia absoluta |
| $$1$$ | $$1$$ |
| $$2$$ | $$3$$ |
| $$3$$ | $$2$$ |
| $$4$$ | $$1$$ |
| $$5$$ | $$1$$ |
| $$6$$ | $$2$$ |
Se puede ver fácilmente que la moda es $$2$$, ya que es el resultado más frecuente del dado.
Las estadísticas de los jugadores de Los Angeles Lakers en el primer partido de las finales de la NBA son las siguientes:
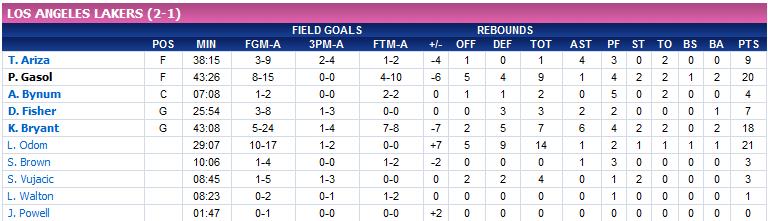
a) ¿Cuál es la moda de puntos anotados (PTS) entre los jugadores de los Lakers?
Se puede observar que en la última columna, la de los puntos, sólo se repite el valor de $$3$$ puntos (los que anotaron S. Brown y S. Vujacic). Así pues, la moda es $$3$$.
b) ¿Y la moda de faltas personales (PF)?
La tabla relativa del número de faltas personales es:
| Faltas personales | Frecuencia absoluta |
| $$0$$ | $$1$$ |
| $$1$$ | $$2$$ |
| $$2$$ | $$2$$ |
| $$3$$ | $$2$$ |
| $$4$$ | $$2$$ |
| $$5$$ | $$1$$ |
Se puede observar que los valores $$1, 2, 3$$ y $$4$$ se dan dos veces, es decir, dos jugadores cometieron $$1$$ falta, otros $$2$$ cometieron $$2$$ faltas, etc. Así pues, la moda de las faltas personales es $$1, 2, 3$$ y $$4$$.