Un quadrat és un paral·lelogram que té els seus quatre costats iguals, així com també té iguals els seus quatre angles, que són rectes. Si diem que la mesura d'un dels seus costats (els altres tres mesuren el mateix) és de 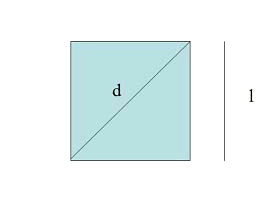$$l$$ unitats (siguin centímetres, decímetres ...)
aleshores l'àrea del quadrat és: $$$A=l^2$$$
I el perímetre, és a dir, la suma de les longituds dels quatre costats és: $$$P=l+l+l+l=4 \cdot l$$$
I si també volem saber la longitud de la seva diagonal, podem aplicar el teorema de Pitàgores i obtenim: $$$l^2+l^2=d^2$$$ $$$2l^2=d^2$$$ $$$d=\sqrt{2 \cdot l^2}= l\cdot \sqrt{2}$$$
Calcular l'àrea d'un quadrat de diagonal $$3$$ cm.
El primer pas és calcular el costat del quadrat. Per fer-ho utilitzarem la fórmula de la diagonal que ens relaciona aquest valor amb el de la longitud del costat:
$$$ 3^2=l^2+l^2=2 \cdot l^2 $$$ $$$l^2=\frac{9}{2}$$$ $$$l=\frac{3}{\sqrt{2}} \ cm$$$
Ara ja podem calcular l'àrea:
$$$A=\Big( \frac{3}{\sqrt{2}}\Big)^2=\frac{9}{2} \ cm^2$$$