Un cuadrado es un paralelogramo que tiene sus cuatro lados iguales así como también tiene iguales sus cuatro ángulos, que son rectos. Si decimos que la medida de uno de sus lados (los otros tres miden lo mismo) es de $$l$$ unidades (sean centímetros, decímetros...)
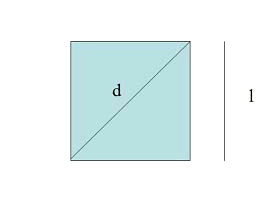
entonces el área del cuadrado es:
$$$A=l^2$$$
Y su perímetro, es decir, la suma de las medidas de sus lados será: $$$P=l+l+l+l=4 \cdot l$$$
Y si también queremos saber la longitud de su diagonal, podemos aplicar el teorema de Pitágoras y obtenemos: $$$l^2+l^2=d^2$$$ $$$2l^2=d^2$$$ $$$d=\sqrt{2 \cdot l^2}= l\cdot \sqrt{2}$$$
Calcular el área de un cuadrado de diagonal $$3$$ cm.
El primer paso es calcular el lado del cuadrado. Para ello utilizaremos la fórmula de la diagonal que nos relaciona dicho valor con la longitud del lado:
$$$ 3^2=l^2+l^2=2 \cdot l^2 $$$ $$$l^2=\frac{9}{2}$$$ $$$l=\frac{3}{\sqrt{2}} \ cm$$$
Ahora ya podemos calcular el área:
$$$A=\Big( \frac{3}{\sqrt{2}}\Big)^2=\frac{9}{2} \ cm^2$$$
