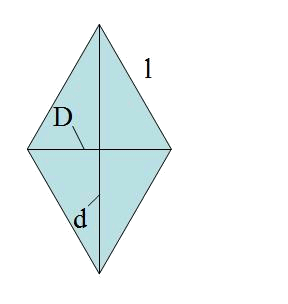
El área del rombo es: $$$A=\frac{D \cdot d}{2}$$$
Su perímetro es: $$$ P=4 \cdot l$$$
Calcular el área de un rombo con $$D = 1 \ m$$ y $$l = 0,7 \ m$$
- Se encuentra $$d$$ utilizando el teorema de Pitágoras a partir de $$D$$ y $$l$$:
$$$ l^2= \Big(\frac{d}{2}\Big)^2 +\Big( \frac {D}{2}\Big)^2 \\ \Big(\frac{d}{2}\Big)^2= l^2-\Big(\frac{D}{2}\Big)^2 \\\Big(\frac{d}{2}\Big)^2=0,7^2 \ m^2-0,5^2 \ m^2=0,24 \ m^2 \\ d= 2 \sqrt{0,24} \ m = 0,98 \ m $$$
- Se encuentra el área: $$$A=\frac{1 \ m \cdot 0'98 \ m}{2}=0,49 \ m^2$$$
Así pues, el área del rombo es: $$0,49 \ m^2$$.
