The area of the square is: $$$A=l^2$$$
Its perimeter is: $$$P=4 \cdot l$$$
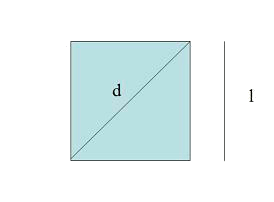
And, applying the Pythagorean theorem, its diagonal is: $$$d=\sqrt{2 \cdot l^2}= l\cdot \sqrt{2}$$$
Calculate the area of a square which diagonal is $$3$$ cm.
- First find the side of the square:
$$$ 3^2=l^2+l^2=2 \cdot l^2 $$$ $$$l^2=\frac{9}{2}$$$ $$$l=\frac{3}{\sqrt{2}} \ cm$$$
- Let's calculate the area:
$$$A=\Big( \frac{3}{\sqrt{2}}\Big)^2=\frac{9}{2} \ cm^2$$$