Funció contínua

Definim una funció $f (x)$ contínua si compleix que per a tot punt del seu domini, la funció és contínua en aquest punt. En una escriptura més formal: $Per a tot x = a pertanyent al D o m (f), lim_{x \to a^{\pm}} f (x) = f (a)$ Observem que en una funció contínua tenim continuïtat i continuïtat lateral en tots els punts.

Atenció: aquesta definició no és equivalent a la de "una funció és contínua si es pot dibuixar sense aixecar el llapis del paper".

Observem el següent exemple per mostrar les diferències:

Exemple

Prenguem la funció $f (x) = \frac{1}{x}$ . Si la representem gràficament tenim:

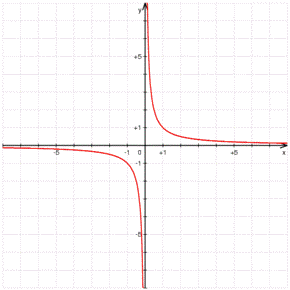
imagen

i podem observar que tenim dues branques diferents que no estan connectades, de manera que podem pensar que la funció no és contínua.

Aquesta funció compleix la definició de continuïtat que hem donat, ja que per a tot punt es compleix la definició, però un pot pensar que en $x = 0$ pugui haver algun problema:

Els límits laterals no coincideixen: $\begin{array}{l} lim_{x \to 0^{+}} f (x) = lim_{x \to 0^{+}} \frac{1}{x} = + \infty \\ lim_{x \to 0^{-}} f (x) = lim_{x \to 0^{-}} \frac{1}{x} = - \infty \end{array}$ però és que la funció no està definida en el punt zero, de manera que no ho podem comparar amb el valor de $f (0)$ .

Si ens fixem, en la definició parlem de continuïtat en tots els punts del seu domini i el zero no forma part del domini d'aquesta funció, així que no té sentit parlar de continuïtat en aquest punt.

Per tant, la funció encara que està separada en dues branques, és contínua.