Angles between straight lines

Two secant straight lines $r$ and $s$ determine four equal angles two by two; this is due to the fact that they are opposite angles in virtue of the apex. The smallest of the angles $α$ and $β$ is defined as the angle between the straight lines $r$ and $s$ .

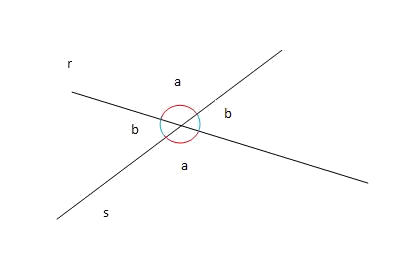
imagen

In case of the drawing, the angle between the straight lines $r$ and $s$ it would be $\hat{r x} = b$ .

A way of determining the above mentioned angle is from the scalar product of the director vectors of the straight lines $r$ and $s$ . Let $\vec{u}$ and $\vec{v}$ be director vectors of the straight lines $r$ and $s$ respectively.

The scalar product of the vectors $\vec{u}$ and $\vec{v}$ is: $\vec{u} \cdot \vec{v} = | \vec{u} | | \vec{v} | \cos \hat{(\vec{u}, \vec{v})}$ Now, let's observe that by taking a vector director of $r$ and one of $s$ , the angle formed by the above mentioned vectors coincides with the angle between both straight lines, if it is acute, or with its supplementary if it is obtuse:

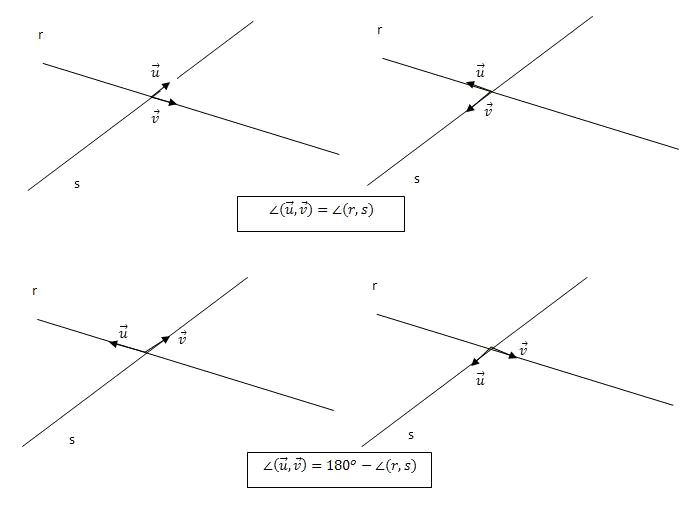
imagen

Therefore, the cosine of the angle between two straight lines will coincide, except for the sign, with that of the angle that its director vectors form, and therefore we have that: $\cos \hat{(r, s)} = | \cos \hat{(\vec{u}, \vec{v})} |$ This last step is because $\cos (a) = - \cos (180 - a)$ This way, if we isolate in the formula of the scalar product, $\cos \hat{(r, s)} = | \cos \hat{(\vec{u}, \vec{v})} | = \frac{| \vec{u} \cdot \vec{v} |}{| \vec{u} | | \vec{v} |}$ Note that: The scalar product between two vectors $\vec{u} = (u_{1}, u_{2})$ and $\vec{v} = (v_{1}, v_{2})$ is defined as $\vec{u} \cdot \vec{v} = u_{1} \cdot v_{1} + u_{2} \cdot v_{2}$ Therefore, if we remember that the expression of the module of a vector is $| \vec{v} | = \sqrt{v_{1}^{2} + v_{2}^{2}}$ We have that in coordinates the expression of the cosine of the angle between two straight lines is: $\cos \hat{(r, s)} = | \cos \hat{(\vec{u}, \vec{v})} | = \frac{| \vec{u} \cdot \vec{v} |}{| \vec{u} | | \vec{v} |} = \frac{| u_{1} \cdot v_{1} + u_{2} \cdot v_{2} |}{\sqrt{u_{1}^{2} + u_{2}^{2}} \sqrt{v_{1}^{2} + v_{2}^{2}}}$

Example

Determine the angle formed by the straight lines $r$ and $s$ , which equations are, respectively, $3 x - 2 y - 1 = 0$ and $- x + 2 y - 3 = 0$ .

Let $\vec{u} = (2, 3)$ and $\vec{v} = (2, 1)$ be director vectors of the straight lines $r$ and $s$ respectively.

Then, applying the previous formula we have $\cos \hat{(r, s)} = | \cos \hat{(\vec{u}, \vec{v})} | = \frac{| \vec{u} \cdot \vec{v} |}{| \vec{u} | | \vec{v} |} = \frac{| u_{1} \cdot v_{1} + u_{2} \cdot v_{2} |}{\sqrt{u_{1}^{2} + u_{2}^{2}} \sqrt{v_{1}^{2} + v_{2}^{2}}} =$ $= \frac{| 2 \cdot 2 + 3 \cdot 1 |}{\sqrt{2^{2} + 3^{2}} \sqrt{2^{2} + 1^{2}}} = \frac{7}{\sqrt{65}}$ Therefore, if we take the calculator we have $\hat{r s} = \arccos (\cos (\hat{r s})) = \arccos (\frac{7}{\sqrt{65}}) = {29.7}^{\circ}$