Angles entre rectes

Dues rectes secants $r$ i $s$ determinen quatre angles iguals dos a dos, això és perquè són angles oposats pel vèrtex. El més petit dels angles $α$ i $β$ es defineix com l'angle entre les rectes $r$ i $s$ .

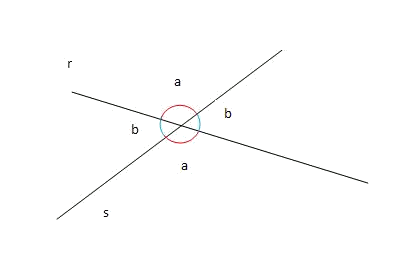
imagen

En el cas del dibuix l'angle entre les rectes $r$ i $s$ seria $\hat{r x} = b$ .

Una manera de determinar aquest angle és a partir del producte escalar dels vectors directors de les rectes $r$ i $s$ . Siguin $\vec{u}$ i $\vec{v}$ vectors directors de les rectes $r$ i $s$ respectivament.

El producte escalar dels vectors $\vec{u}$ i $\vec{v}$ és: $\vec{u} \cdot \vec{v} = | \vec{u} | | \vec{v} | \cos \hat{(\vec{u}, \vec{v})}$ Ara, fixem-nos que prenent un vector director de $r$ i un de $s$ , l'angle format per aquests vectors coincideix amb l'angle entre les dues rectes, si és agut, o bé amb el seu suplementari si és obtús:

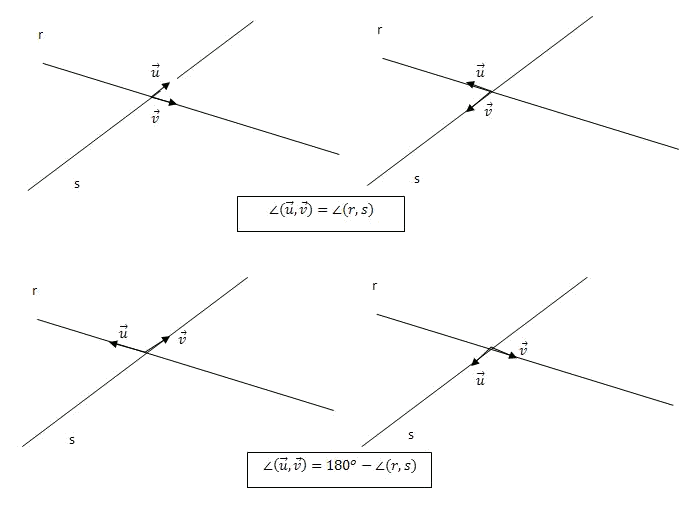
imagen

Per tant, el cosinus de l'angle entre les dues rectes coincidirà, exceptuant el signe, amb el de l'angle que formen els seus vectors directors, i per tant tenim que: $\cos \hat{(r, s)} = | \cos \hat{(\vec{u}, \vec{v})} |$ Aquest últim pas és degut a que $\cos (a) = - \cos (180 - a)$ Així, si aïllem a la fórmula del producte escalar, $\cos \hat{(r, s)} = | \cos \hat{(\vec{u}, \vec{v})} | = \frac{| \vec{u} \cdot \vec{v} |}{| \vec{u} | | \vec{v} |}$ Nota: El producte escalar entre dos vectors $\vec{u} = (u_{1}, u_{2})$ i $\vec{v} = (v_{1}, v_{2})$ es defineix com $\vec{u} \cdot \vec{v} = u_{1} \cdot v_{1} + u_{2} \cdot v_{2}$ Per tant, si recordem que l'expressió del mòdul d'un vector és $| \vec{v} | = \sqrt{v_{1}^{2} + v_{2}^{2}}$ Tenim que en coordenades l'expressió del cosinus de l'angle entre dues rectes és: $\cos \hat{(r, s)} = | \cos \hat{(\vec{u}, \vec{v})} | = \frac{| \vec{u} \cdot \vec{v} |}{| \vec{u} | | \vec{v} |} = \frac{| u_{1} \cdot v_{1} + u_{2} \cdot v_{2} |}{\sqrt{u_{1}^{2} + u_{2}^{2}} \sqrt{v_{1}^{2} + v_{2}^{2}}}$

Exemple

Determina l'angle format per les rectes $r$ i $s$ , les equacions de les quals són, respectivament, $3 x - 2 y - 1 = 0$ i $- x + 2 y - 3 = 0$ .

Siguin $\vec{u} = (2, 3)$ i $\vec{v} = (2, 1)$ vectors directors de les rectes $r$ i $s$ respectivament.

Llavors, aplicant la fórmula anterior tenim $\cos \hat{(r, s)} = | \cos \hat{(\vec{u}, \vec{v})} | = \frac{| \vec{u} \cdot \vec{v} |}{| \vec{u} | | \vec{v} |} = \frac{| u_{1} \cdot v_{1} + u_{2} \cdot v_{2} |}{\sqrt{u_{1}^{2} + u_{2}^{2}} \sqrt{v_{1}^{2} + v_{2}^{2}}} =$ $= \frac{| 2 \cdot 2 + 3 \cdot 1 |}{\sqrt{2^{2} + 3^{2}} \sqrt{2^{2} + 1^{2}}} = \frac{7}{\sqrt{65}}$ Per tant, si agafem la calculadora tenim que: $\hat{r s} = \arccos (\cos (\hat{r s})) = \arccos (\frac{7}{\sqrt{65}}) = {29.7}^{\circ}$