Posicions relatives entre rectes

Dues rectes en el pla poden ser secants, paral·leles o coincidents.

El següent dibuix mostra les 3 possibles situacions:

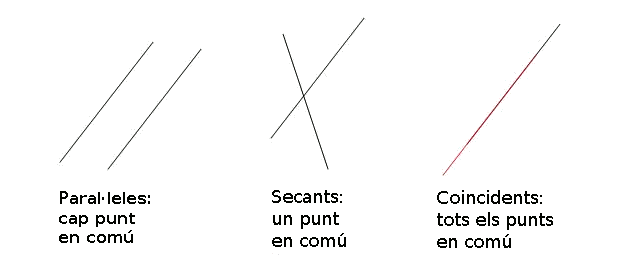
imagen

Vegem com distingir entre els tres casos. Cal comentar que hi ha múltiples maneres de fer-ho segons l'equació de la recta que tinguem. Evidentment totes elles seran equivalents i si sabem com passar d'una equació de la recta a una altra, qualsevol mètode dels següents ens servirà.

Vegem una forma geomètrica d'abordar el problema i una forma algebraica.

Des d'un punt de vista geomètric, si considerem dues rectes coincidents com un cas particular de paral·lelisme, tenim que dues rectes en el pla poden ser únicament paral·leles o secants.

Quan dues rectes són paral·leles?

Quan els seus vectors directors són paral·lels.

Quan dos vectors són paral·lels?

Quan un és proporcional a l'altre. És a dir, si tenim els vectors $\vec{u}$ i $\vec{v}$ , han de ser tals que $\vec{u} = k \cdot \vec{v}$ on $k$ pot ser un nombre real qualsevol.

En coordenades, si $\vec{u} = (u_{1}, u_{2})$ i $\vec{v} = (v_{1}, v_{2})$ els vectors són proporcionals i per tant paral·lels si i només si $\frac{u_{1}}{v_{1}} = \frac{u_{2}}{v_{2}}$

Per tant, ja tenim una manera geomètrica de trobar la posició relativa de dues rectes, veient si els seus vectors directors són paral·lels o no:

Vectors directors paral·lels:
- Si la rectes tenen un punt en comú són coincidents i són la mateixa.
- Si les rectes no tenen cap punt en comú són paral·leles.
Vectors directors no paral·lels: Les rectes són secants.

És important notar que en general, dues rectes paral·leles tenen vectors directors de components proporcionals i pendents iguals.

Exemple

Donades les rectes $r$ i $s$ , amb equacions respectivament $y = 2 x - 7$ i $\frac{x - 1}{3} = \frac{y - 2}{5}$ , trobeu la posició relativa entre elles i en cas que fossin secants, el punt de tall:

D'entrada busquem vectors directors de les dues rectes.

Per $y = 2 x - 7$ tenim que el pendent és $m = 2$ . Per tant $\vec{u} = (1, 2)$ és un vector director de la recta $r$ .

Per $\frac{x - 1}{3} = \frac{y - 2}{5}$ tenim que $\vec{v} = (3, 5)$ és un vector director de la recta $s$ .

Per tant, si dividim component a component tenim: $\frac{u_{1}}{v_{1}} = \frac{1}{3} \neq \frac{2}{5} = \frac{u_{2}}{v_{2}}$ i per tant els vectors directors no són paral·lels i les rectes són secants.

Resolem el sistema d'equacions format per les equacions de les dues rectes per trobar el punt de tall:

${\begin{matrix} y = 2 x - 7 \\ \frac{x - 1}{3} = \frac{y - 2}{5} \end{matrix} \Leftrightarrow {\begin{matrix} y = 2 x - 7 \\ \frac{x - 1}{3} = \frac{2 x - 7 - 2}{5} \end{matrix} \Leftrightarrow$ $\Leftrightarrow {\begin{matrix} y = 2 x - 7 \\ 5 x - 5 = 6 x - 27 \end{matrix} \Leftrightarrow {\begin{matrix} y = 2 x - 7 \\ x = 22 \end{matrix} \Leftrightarrow {\begin{matrix} y = 37 \\ x = 22 \end{matrix}$

Per tant el punt de tall entre les dues rectes és $P = (22, 37)$

Des d'un punt de vista més algebraic, podem analitzar la posició relativa de dues rectes $r$ i $s$ , a partir del nombre de solucions del sistema de dues equacions que formen les expressions de les rectes $r$ i $s$ .

Per exemple, si considerem dues rectes $r$ i $s$ , i les seves respectives equacions implícites:

${\begin{cases} r : a x + b y + c = 0 \\ s : a^{'} x + b^{'} y + c^{'} = 0 \end{cases}$

Tenim que el sistema d'equacions:

${\begin{cases} a x + b y + c = 0 \\ a^{'} x + b^{'} y + c^{'} = 0 \end{cases}$

té per solució els punts d'intersecció entre les rectes $r$ i $s$ . Per tant,

Si el sistema no té solució, les rectes són paral·leles.
Si el sistema té infinites solucions, les rectes són coincidents.
Si el sistema té 1 solució, les rectes són secants.

Exemple

Donats els següents parells de rectes, trobeu la posició relativa entre elles.

a) ${\begin{matrix} - x + y = - 1 \\ 2 x + 3 y + 3 = 0 \end{matrix}$

Resolem el sistema d'equacions: ${\begin{matrix} - x + y = - 1 \\ 2 x + 3 y + 3 = 0 \end{matrix} \Leftrightarrow {\begin{matrix} - 2 x + 2 y = - 2 \\ 2 x + 3 y = - 3 \end{matrix} \Leftrightarrow {\begin{array}{rcl} - 2 x + 2 y = - 2 \\ + & \underset{―}{2 x + 3 y = - 3} \\ 0 + 5 y = - 5 \end{array}$

I la solució del sistema és $x = 0, y = - 1$ . El fet que la solució sigui única ens indica que les rectes són secants i el punt de tall és la solució del sistema.

b) ${\begin{matrix} x + 2 y = 2 \\ 2 x + 4 y + 1 = 0 \end{matrix}$

Resolem el sistema d'equacions: ${\begin{matrix} x + 2 y = 2 \\ 2 x + 4 y + 1 = 0 \end{matrix} \Leftrightarrow {\begin{matrix} - 2 x - 4 y = - 4 \\ 2 x + 4 y = - 1 \end{matrix} \Leftrightarrow {\begin{array}{rcl} - 2 x - 4 y = - 4 \\ + & \underset{―}{2 x + 4 y = - 1} \\ 0 = - 5 \end{array}$

I com el sistema no té solució podem concloure que les dues rectes són paral·leles.

c) ${\begin{matrix} - x + y = 1 \\ 2 x - 2 y = - 2 \end{matrix}$

Resolem el sistema d'equacions: ${\begin{matrix} - x + y = 1 \\ 2 x - 2 y = - 2 \end{matrix} \Leftrightarrow {\begin{matrix} - 2 x + 2 y = 2 \\ 2 x - 2 y = - 2 \end{matrix} \Leftrightarrow {\begin{array}{rcl} - 2 x + 2 y = 2 \\ + & \underset{―}{2 x - 2 y = - 2} \\ 0 = 0 \end{array}$

I com el sistema té infinites solucions, les dues rectes han de ser coincidents.