Coordenades d'un punt, components d'un vector i punt mitjà d'un segment

Coordenades d'un punt al pla

Vegem com s'utilitzen els vectors per assignar coordenades als punts del pla.

Considerem un punt fix del pla $O$ (conegut com a origen), i una base $B = {\vec{u}, \vec{v}}$ de $V_{2}$ (Espai vectorial de dimensió 2).

Recordem que una base de $V_{2}$ són dos vectors linealment independents. El conjunt format per $O$ i $B = {\vec{u}, \vec{v}}$ constitueix un sistema de referència al pla, ja que permet determinar la posició de qualsevol altre punt del pla.

Això és degut a que qualsevol altre punt $P$ del pla determina amb el punt $O$ un vector $\vec{O P}$ . Siguin $(p_{1}, p_{2})$ les components del vector en la base $B$ . Llavors $(p_{1}, p_{2})$ són les coordenades del punt $P$ en el sistema de referència $R = {O; \vec{u}, \vec{v}}$ i escrivim $P = (p_{1}, p_{2})$ .

El procediment per trobar les coordenades d'un punt $P$ en un sistema de referència donat és el següent:

A partir dels punts $O$ i $P$ determinem el vector $\vec{O P}$
Expressem el vector $\vec{O P}$ com a combinació lineal dels vectors de la base $B = {\vec{u}, \vec{v}}$ , és a dir, $\vec{O P} = p_{1} \cdot \vec{u} + p_{2} \cdot \vec{v}$
$P = (p_{1}, p_{2})$

Exemple

Expressar el punt $P$ del dibuix en el sistema de referència $R = {O; \vec{u}, \vec{v}}$ .

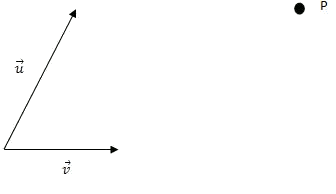
imagen

Dibuixem el vector $\vec{O P}$ :

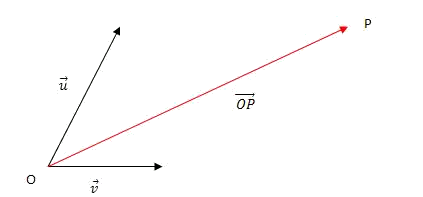
imagen

Expressem el vector $\vec{O P}$ com a combinació lineal dels vectors de la base $B = {\vec{u}, \vec{v}}$ :

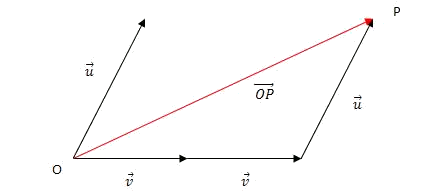
imagen

Obtenim $\vec{O P} = \vec{u} + 2 \vec{v}$ i per tant les coordenades del punt $P$ són $P = (1, 2)$

D'ara endavant considerarem com a sistema de referència $R$ , el format per l'origen de coordenades $O = (0, 0)$ i la base canònica de $V_{2}$ $B = {\vec{i}, \vec{j}}$ .

Components d'un vector determinat per dos punts

Vegem ara la forma de determinar les components d'un vector si sabem les coordenades dels seus extrems.

Siguin $P = (p_{1}, p_{2})$ i $Q = (q_{1}, q_{2})$ dos punts del pla, i sigui $\vec{P Q}$ el vector que va de $P$ a $Q$ . Llavors les components del vector $\vec{P Q}$ són $\vec{P Q} = (q_{1} - p_{1}, q_{2} - p_{2})$ .

Exemple

Siguin $P = (2, 6)$ i $Q = (- 3, 9)$ . Les components del vector $\vec{P Q}$ són: $\vec{P Q} = (- 3 - 2, 9 - 6) = (- 5, 3)$

Aplicar un vector a un punt

Donats un punt $P$ i un vector $\vec{v}$ , el resultat d'aplicar el vector al punt és un nou punt $Q$ situat en la direcció de $\vec{v}$ i a una distància $| \vec{v} |$ . (Mòdul del vector $\vec{v}$ )

Les coordenades d'aquest nou punt $Q$ es calculen a partir de les de $P = (p_{1}, p_{2})$ i $\vec{v} = (v_{1}, v_{2})$ com $Q = P + \vec{v} = (p_{1} + v_{1}, p_{2} + v_{2})$

NOTA: És molt important tenir present que aquesta operació de "suma" només té sentit entre un punt i un vector. MAI hem de sumar dos punts, i el resultat de sumar dos vectors és un altre vector i no un punt!

Exemple

Donada la següent figura, determinar les coordenades del punt $P$ de la figura resultat d'aplicar el vector $\vec{v}$ al punt $A$ .

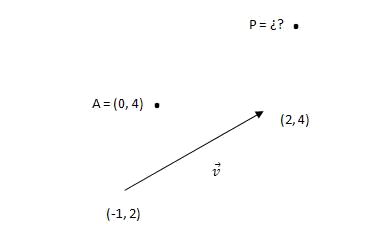
imagen

Comencem calculant les components del vector $\vec{v}$ : $\vec{v} = (2 - (- 1), 4 - 2) = (3, 2)$ Com $P$ és el resultat d'aplicar el vector $\vec{v}$ al punt $A$ es té, $P = A + \vec{v} = (0, 4) + (3, 2) = (3, 6)$

Punt mitjà d'un segment

Considerem ara el segment d'extrems $A = (a_{1}, a_{2})$ i $B = (b_{1}, b_{2})$ . Sigui $M = (m_{1}, m_{2})$ el punt mitjà d'aquest segment. Evidentment aquest punt compleix que $\vec{A B} = 2 \cdot \vec{A M}$ , és a dir que $(b_{1} - a_{1}, b_{2} - a_{2}) = 2 \cdot (m_{1} - a_{1}, m_{2} - a_{2})$

Separant component a component obtenim: $\begin{array}{rcl} b_{1} - a_{1} & = & 2 \cdot (m_{1} - a_{1}) \\ b_{2} - a_{2} & = & 2 \cdot (m_{2} - a_{2}) \end{array}$ i aïllant tenim: $\begin{array}{rcl} m_{1} & = & \frac{a_{1} + b_{1}}{2} \\ m_{2} & = & \frac{a_{2} + b_{2}}{2} \end{array}$ De manera que podem calcular les coordenades del punt mitjà d'un segment a partir de les coordenades dels seus extrems.

Exemple

Donats els punts $A = (- 3, 7)$ i $B = (1, 2)$ trobeu el punt mitjà del segment que determinen.

Aplicant les fórmules anteriors tenim: $\begin{array}{rcl} m_{1} & = & \frac{a_{1} + b_{1}}{2} = \frac{- 3 + 2}{2} = - 1 \\ m_{2} & = & \frac{a_{2} + b_{2}}{2} = \frac{7 + 2}{2} = \frac{9}{2} \end{array}$ Per tant el punt mitjà del segment $A B$ és $M = (- 1, \frac{9}{2})$