Coordenadas de un punto en el plano
Veamos como se utilizan los vectores para asignar coordenadas a los puntos del plano.
Consideramos un punto fijo del plano
Recordemos que una base de
Esto se debe al hecho que cualquier otro punto
El procedimiento para encontrar las coordenadas de un punto
-
A partir de los puntos
-
Expresamos el vector
Ejemplo
Expresar el punto
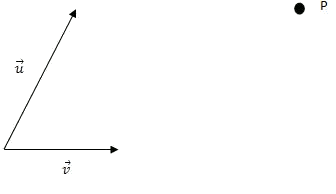
- Dibujamos el vector
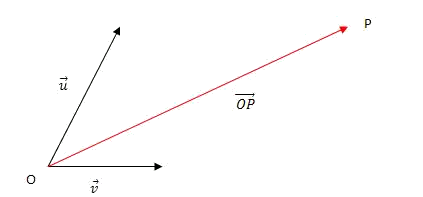
- Expresamos el vector
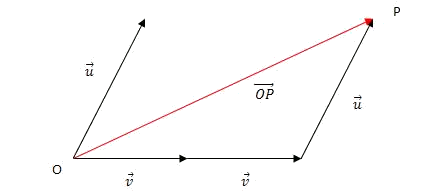
- Obtenemos
De ahora en adelante consideraremos como sistema de referencia
Componentes de un vector determinado por dos puntos
Veamos ahora la forma de determinar las componentes de un vector si sabemos las coordenadas de sus extremos:
Sean
Ejemplo
Sean
Aplicar un vector a un punto
Dados un punto
Las coordenadas de este nuevo punto
NOTA: Es muy importante tener presente que esta operación de "suma" sólo tiene sentido entre un punto y un vector. NUNCA debemos sumar dos puntos, y el resultado de sumar dos vectores es otro vector y no un punto!
Ejemplo
Dada la siguiente figura, determinar las coordenadas del punto
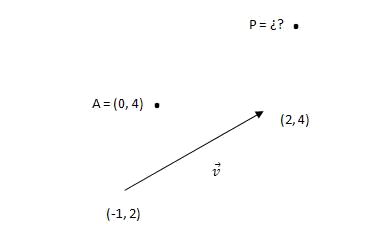
Empezamos calculando las componentes del vector
Punto medio de un segmento
Consideremos ahora el segmento de extremos
Separando componente a componente obtenemos:
Ejemplo
Dados los puntos
Aplicando las fórmulas anteriores tenemos:
