Ángulos entre rectas

Dos rectas secantes $r$ y $s$ determinan cuatro ángulos iguales dos a dos; esto se debe a que son ángulos opuestos por el vértice. El más pequeño de los ángulos $α$ y $β$ se define como el ángulo entre las rectas $r$ y $s$ .

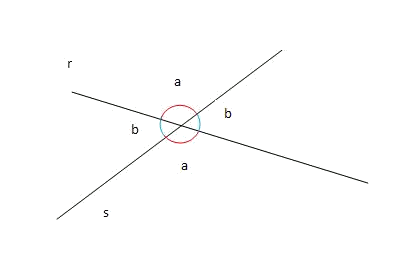
imagen

En el caso del dibujo el ángulo entre las rectas $r$ y $s$ sería $\hat{r x} = b$ .

Una forma de determinar dicho ángulo es a partir del producto escalar de los vectores directores de las rectas $r$ y $s$ . Sean $\vec{u}$ y $\vec{v}$ vectores directores de las rectas $r$ y $s$ respectivamente.

El producto escalar de los vectores $\vec{u}$ y $\vec{v}$ es: $\vec{u} \cdot \vec{v} = | \vec{u} | | \vec{v} | \cos \hat{(\vec{u}, \vec{v})}$ Ahora, fijémonos que tomando un vector director de $r$ y uno de $s$ , el ángulo formado por dichos vectores coincide con el ángulo entre las dos rectas, si es agudo, o bien con su suplementario si es obtuso:

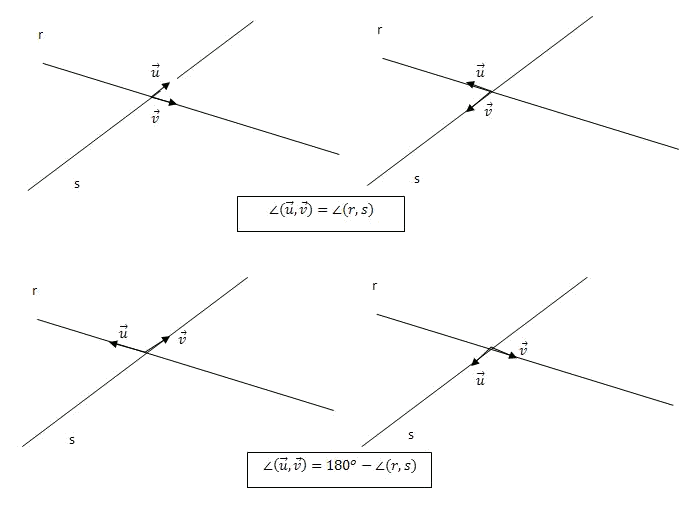
imagen

Por tanto, el coseno del ángulo entre las dos rectas coincidirá, exceptuando el signo, con el del ángulo que forman sus vectores directores, y por tanto tenemos que: $\cos \hat{(r, s)} = | \cos \hat{(\vec{u}, \vec{v})} |$ Este último paso se debe a que $\cos (a) = - \cos (180 - a)$ Así, si aislamos en la formula del producto escalar, $\cos \hat{(r, s)} = | \cos \hat{(\vec{u}, \vec{v})} | = \frac{| \vec{u} \cdot \vec{v} |}{| \vec{u} | | \vec{v} |}$

Nota: El producto escalar entre dos vectores $\vec{u} = (u_{1}, u_{2})$ y $\vec{v} = (v_{1}, v_{2})$ se define cómo $\vec{u} \cdot \vec{v} = u_{1} \cdot v_{1} + u_{2} \cdot v_{2}$ Por tanto, si recordamos que la expresión del módulo de un vector es $| \vec{v} | = \sqrt{v_{1}^{2} + v_{2}^{2}}$ Tenemos que en coordenadas la expresión del coseno del ángulo entre dos rectas es: $\cos \hat{(r, s)} = | \cos \hat{(\vec{u}, \vec{v})} | = \frac{| \vec{u} \cdot \vec{v} |}{| \vec{u} | | \vec{v} |} = \frac{| u_{1} \cdot v_{1} + u_{2} \cdot v_{2} |}{\sqrt{u_{1}^{2} + u_{2}^{2}} \sqrt{v_{1}^{2} + v_{2}^{2}}}$

Ejemplo

Determina el ángulo formado por las rectas $r$ y $s$ , cuyas ecuaciones son, respectivamente, $3 x - 2 y - 1 = 0$ y $- x + 2 y - 3 = 0$ .

Sean $\vec{u} = (2, 3)$ y $\vec{v} = (2, 1)$ vectores directores de las rectas $r$ y $s$ respectivamente.

Entonces, aplicando la fórmula anterior tenemos $\cos \hat{(r, s)} = | \cos \hat{(\vec{u}, \vec{v})} | = \frac{| \vec{u} \cdot \vec{v} |}{| \vec{u} | | \vec{v} |} = \frac{| u_{1} \cdot v_{1} + u_{2} \cdot v_{2} |}{\sqrt{u_{1}^{2} + u_{2}^{2}} \sqrt{v_{1}^{2} + v_{2}^{2}}} =$ $= \frac{| 2 \cdot 2 + 3 \cdot 1 |}{\sqrt{2^{2} + 3^{2}} \sqrt{2^{2} + 1^{2}}} = \frac{7}{\sqrt{65}}$ Por tanto, si cogemos la calculadora tenemos que $\hat{r s} = \arccos (\cos (\hat{r s})) = \arccos (\frac{7}{\sqrt{65}}) = {29.7}^{\circ}$