Coordinates of a point on the plane
Let's see how vectors are used to assign coordinates to the points in the plane.
We consider a fixed point in the plane
Let's remember that a basis of
This is because any other points
The procedure to find the coordinates of point
-
From the points
-
We express the vector
Example
Express point
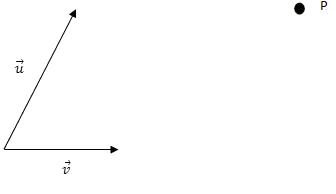
- We draw the vector
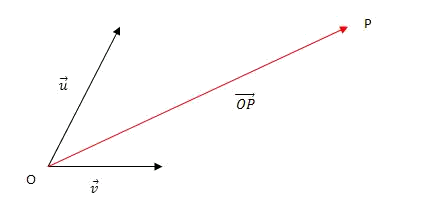
- We express the vector
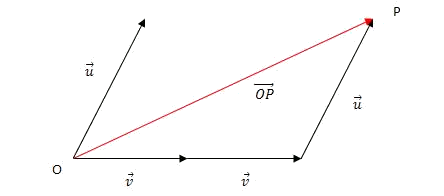
- We obtain
From now on we will consider, as reference system
Components of a vector determined by two points
Let's see now the way to determine the components of a vector if we know the coordinates of its endpoints:
Let
Example
Given
Applying a vector to a point
Given a point
The coordinates of this new point
NOTE: It is very important to bear in mind that this addition operation only makes sense between a point and a vector. We must never add two points, and the result of adding two vectors is another vector and not a point!
Example
Considering the following figure, determine the coordinates of point
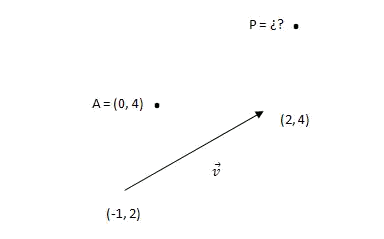
We begin by calculating the components of the vector
Midpoint of a segment
Let's consider now a segment with endpoints
Separating component by component we obtain:
Example
Considering the points
Applying the previous formulas we have:
