Concept and equation of a function

Concept of function

A function is a relation between two sets which satisy that for every element of the domain one and only one element in the codomain is assigned. We can understand the function as a machine that transforms an element of the first set (domain) into an element of the other set (codomain). A useful way of representing the functions are the well-known Venn diagrams. We observe that to every element of the domain A, an element of the codomain B is assigned to it:

f:

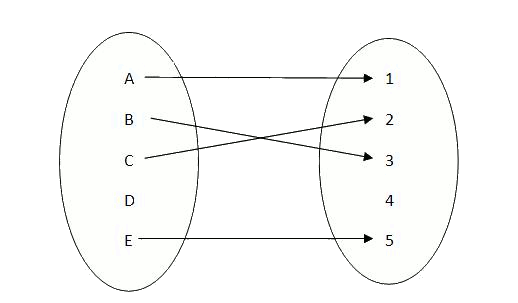
imagen

To see the difference between what a function is and is not, we can observe the following figure:

g:

imagen

This way, while the first relation f is a function, since it assigns only one element of the codomain to every element of the domain, the relation g is not a function since there exist elements of the domain to which are assigned more than one element of the codomain.

The set of inputs receives the name of domain, and the set of outputs the name of codomain.

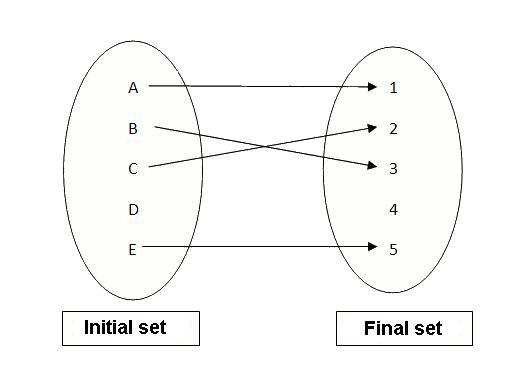
imagen

The values of the initial set to which we can apply the function constitute the domain of the function. The elements of the set of outputs that we can obtain after applying the function to an element of the domain constitute the codomain (or image set) of the function.

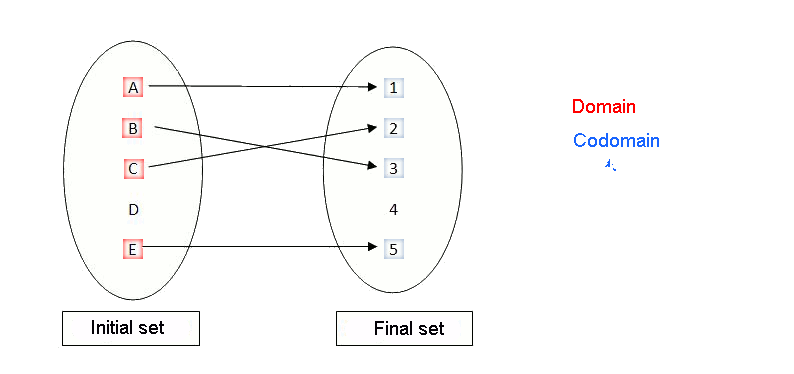
imagen

The elements of the domain are called antiimages, and those of the image, images.

Example

Let's imagine that to prepare a rice dish, we put three cups of rice for every two people plus two cups "extra" if someone wants to have seconds. We can represent this relation in the following way:number rice cups =32⋅ number people +2We observe that the initial set will be the set of natural numbers and that positive fractions will be the set of images. Therefore:

Initial set =N=1,2,3,4,5...

Final set=Q+={12,23,25,3,72,94,103,125,…}

In this function, the domain coincides with the set of antiimages. On the other hand, the image is only a subset of the rational positives. This is translated into:

Dom (f)=N

Im(f)={72,5,132,8,192,11,…}

Finally, if we want to know how many cups of rice we need for 10 people, we have to ask ourselves what the image of 10 is, that is to say, f(10): f(10)=32⋅10+2=17

Therefore, we need 17 rice cups for 10 people.

On the other hand, if we know that we have put 15,5 cups of rice we ask ourselves the number of people that the rice will ce, what we are actually wondering is the value of the antiimage of 15,5, that is to say f−1(15,5): 15,5=32x+213.5=32xx=2⋅13.53=9

Therefore the rice was for 9 people and f−1(15,5)=9.

Equation of a function

The equation of a function is the algebraic expression that summarizes how one can obtain the values of the final set from the values of the initial set.

Example

Considering the function f defined by doing the third part and reducing two to an integer, the equation of such a function is:

f(x)=x3−2

The values that can take the elements of the domain of the function is: the independent variable . Generally, it is denoted by x. In the previous example,x∈Z since in this case the statement specifies it.

This is called the dependent variable, the set of values that the images may take. Generally, it is denoted by the letter y, where y=f(x).

Example

In the previous example, y∈{−2,−53,−73,−43,−83,−1,…}⊂Q