A polynomial function is a function whose analytic expression is given by a polynomial: $$$f(x)=a_nx^n+a_{n-1}x^{n-1}+\ldots+a_1x+a_0$$$ with $$n \in \mathbb{N}\cup \{0\}$$, $$a_n,a_{n-1},\ldots, a_1,,_a0 \in \mathbb{R}$$ and $$a_n\neq 0$$ if $$n\neq 0$$.
Since the polynomials can be evaluated in any real number, we have that the domain of the polynomial functions is $$\mathbb{R}$$, that is $$Dom(f)=\mathbb{R}$$.
The image of this type of functions is not always clear:
- Polynomials of odd degree: This is the simplest case since $$Im(f)=\mathbb{R}$$.
- Polynomial of even degree: The image will depend on the coefficients of the polynomial, which will determine its orientation and its relative extrema. In the case $$n = 2$$, which we will call quadratic functions, it is enough to know the vertex of the parabola and to take into account the sign of the first coefficient.
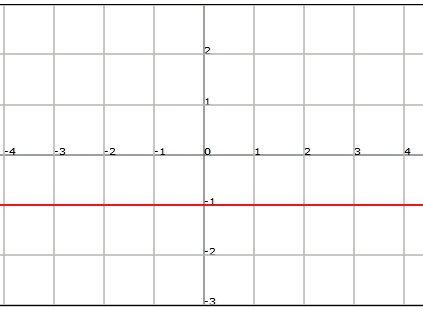
Constant function: $$f (x) = k$$
This is a polynomial of degree $$0$$. Its graph is a horizontal straight line that goes along the point where $$y=k$$ (and therefore $$Im (f) = k$$).
An example of constant function is $$f (x) =-1$$:
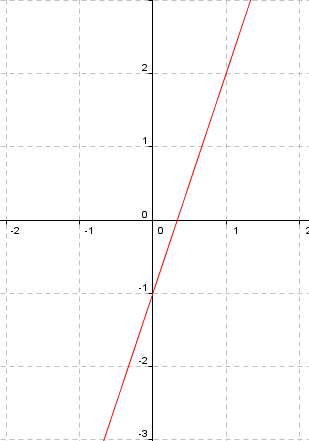
Affine function: $$f (x) = ax + b$$
In order to have a linear function we need $$a\neq 0$$. The degree of this function is $$1$$. Its graph is a straight line that goes through the point $$(0, b)$$ and its slope depends on the value of $$a$$.
In the particular case in which $$b = 0$$, we will call it a linear function: $$f (x) = ax$$. This function is equivalent to the function of direct proportionality, where $$a$$ is the proportionality constant.
In the particular case in which $$a = 1$$, we obtain the identity function, that is, $$f (x) = x$$ , whose graph is the $$45$$ degree line.
An example of affine function is $$f (x) = 3x - 1$$.
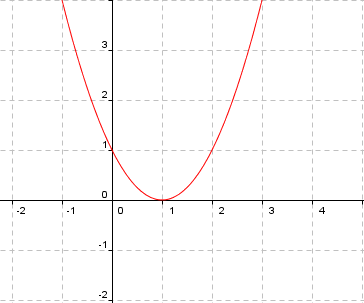
Quadratic function:$$f (x) = ax^2 + bx + c$$
To be a quadratic function it is necessary to have $$a\neq 0$$. This is a function of second degree, whose graph is an $$\cup$$ shaped parabola if $$a> 0$$, or an $$\cap$$ shaped parabola if $$a <0$$ (see the unit on convexity and concavity).
The vertex of the above mentioned parabola is $$\displaystyle \Big(-\frac{b}{2a}, -\frac{b^2-4ac}{4a}\Big)$$.
The intersection point with the vertical axis is $$c$$. The points cutting through the horizontal axis are the solutions to the equation of the second degree if they exist.
An example of quadratic function is $$f(x) =x^2-2x+1$$.