Una función polinómica es una función cuya expresión analítica viene dada por un polinomio: $$$f(x)=a_nx^n+a_{n-1}x^{n-1}+\ldots+a_1x+a_0$$$ con $$n \in \mathbb{N}\cup \{0\}$$, $$a_n,a_{n-1},\ldots, a_1,,_a0 \in \mathbb{R}$$ y $$a_n\neq 0$$ si $$n\neq 0$$.
Como los polinomios pueden ser evaluados en cualquier número real, tenemos que el dominio de las funciones polinómicas es todo $$\mathbb{R}$$, es decir $$Dom(f)=\mathbb{R}$$.
La imagen de este tipo de funciones no siempre es evidente:
- Polinomio de grado impar: Este es el caso sencillo ya que $$Im(f)=\mathbb{R}$$.
- Polinomio de grado par: La imagen dependerá de los coeficientes del polinomio, que determinarán orientación y extremos relativos. En el caso $$n = 2$$, es decir funciones cuadráticas, basta con conocer el vértice de la parábola y tener en cuenta su orientación.
Función constante: $$f (x) = k$$
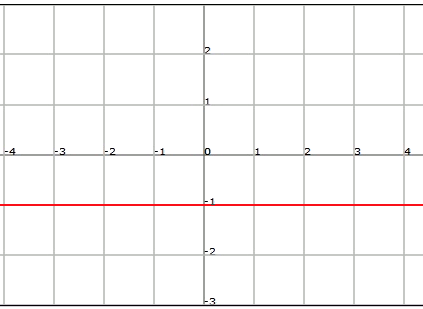
Se trata de una función polinómica de grado $$0$$. Su gráfica es una recta horizontal que pasa por todos los puntos de ordenada $$y=k$$ (y por tanto $$Im (f) = k$$).
Un ejemplo de función constante es $$f (x) =-1$$:
Función afín: $$f (x) = ax + b$$
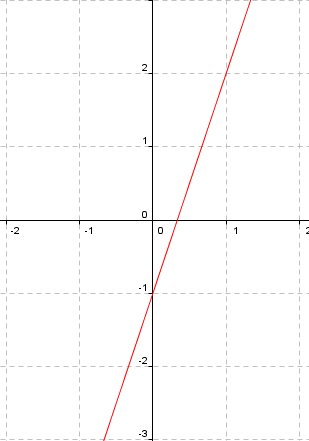
Un requisito es que sea $$a\neq 0$$. Se trata de una función polinómica de grado $$1$$. Su gráfica es una recta que pasa por el punto $$(0, b)$$ y cuya inclinación depende del valor de $$a$$ (también conocido cómo pendiente).
En el caso particular en que $$b = 0$$, se tiene la conocida como función lineal: $$f (x) = ax$$. Esta función es equivalente a la función de proporcionalidad directa, donde $$a$$ es la constante de proporcionalidad.
En el caso particular en que $$a = 1$$, obtenemos la función identidad, es decir, $$f (x) = x$$ , cuya gráfica es la bisectriz del primer y del tercer cuadrante.
Un ejemplo de función afín es $$f (x) = 3x - 1$$.
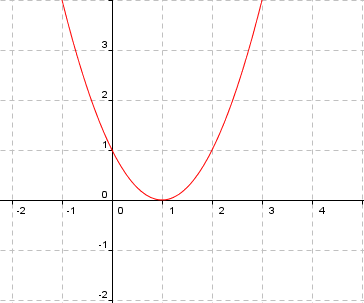
Función cuadrática: $$f (x) = ax^2 + bx + c$$
Para obtener una función cuadrática es necesario que $$a\neq 0$$. Se trata de una función polinómica de segundo grado, cuya gráfica es una parábola abierta hacia arriba si $$a> 0$$, o bien hacia abajo si $$a <0$$.
El vértice de dicha parábola es $$\displaystyle \Big(-\frac{b}{2a}, -\frac{b^2-4ac}{4a}\Big)$$.
El punto de corte con el eje vertical es $$c$$. Los puntos de corte con el eje horizontal son las soluciones de la ecuación de segundo grado correspondiente.
Un ejemplo de función cuadrática es $$f(x) =x^2-2x+1$$.