Una función definida a trozos es una función cuya expresión analítica no es única sino que depende del valor de la variable independiente.
Así la función definida por $$$f(x)=\left\{\begin{array}{rcl} -x-1 & \mbox{ si } & x \leq -3 \\ 3 & \mbox{ si } & -1 < x < 1 \\ x-2 & \mbox{ si } & x\geq 1 \end{array}\right.=\left\{\begin{array}{rcl} -x-1 & \mbox{ si } & x\in (-\infty,3] \\ 3 & \mbox{ si } & x\in (-1,1)\\ x-2 & \mbox{ si } & x\in [1, +\infty]\end{array}\right.$$$ es una función definida a trozos.
Para calcular la imagen de un elemento $$x$$ observamos a qué intervalo pertenece y lo sustituimos en la expresión analítica correspondiente a este intervalo.
En el caso anterior por ejemplo,
- si $$x=-4$$, sustituimos en $$f(x)=-x-1$$ y obtenemos $$f(-4)=3$$
- si $$x=-2$$, la imagen no está definida ya que $$-2$$ no pertenece a ningún intervalo de definición de la función.
- si $$x=0.5$$, sustituimos en $$f(x)=3$$ obteniendo $$f(0.5)=3$$
- si $$x=1$$ sustituimos en $$f(X)=x-2$$ obteniendo $$f(1)=-1$$
Como las expresiones que definen cada uno de los trozos tienen como dominio al menos el propio trozo, el dominio de la función $$f(x)$$ está formado por la unión de los intervalos de definición de la función. $$$Dom(f)=(-\infty,-3] \cup (-1,1)\cup [1,+\infty)=(-\infty,-3]\cup (-1,+ \infty)$$$ Si nos fijamos ahora en el gráfico de la función anterior que presentamos a continuación, podemos observar que $$Im (f)=[-1,+\infty)$$:
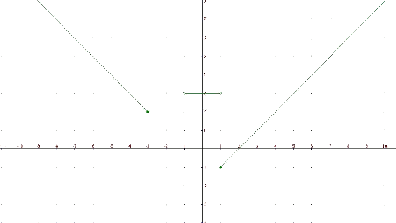
Veamos unos ejemplos de funciones definidas a trozos:
Consideramos la función $$\displaystyle f(x)=\left\{\begin{array}{rcl} 1 & \mbox{ si } & x\leq 2 \\ 2 & \mbox{ si } & x > 2\end{array}\right.$$.
Su gráfica es la unión de las gráficas de las funciones $$f(x)=1$$ para $$x \leq 2$$ y $$f(x)=2$$ para $$x>2$$.
La representación gráfica sería:
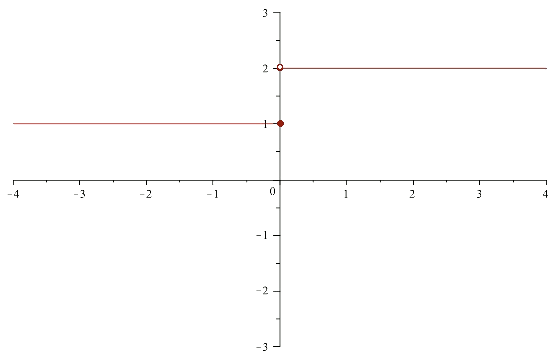
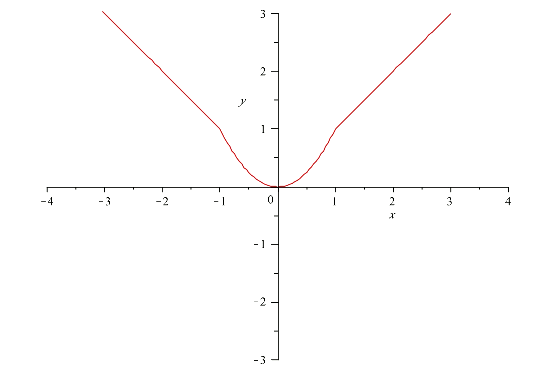
Consideramos la función $$\displaystyle f(x)=\left\{\begin{array}{rcl} -x & \mbox{ si } & x\leq -1 \\ x^2 & \mbox{ si } & -1 < x < 1 \\ x & \mbox{ si } & x \geq 1 \end{array}\right.$$
Esta vez su gráfica será la unión de una recta, una parábola y otra recta, definidas cada una donde indica la función.
$$\displaystyle f(x)=\left\{\begin{array}{rcl} 2x-1 & \mbox{ si } & x < 1 \\ x+3 & \mbox{ si } & x > 1 \end{array}\right.$$
y si queremos evaluar en $$x=-1$$ obtendremos: $$f(-1)=f_1(-1)=2(-1)=2(-1)-1=-2-1=-3$$
$$\displaystyle f(x)=\left\{\begin{array}{rcl} x-1 & \mbox{ si } & x<-3 \\ x^2+1 & \mbox{ si } & -3\leq < 0 \\ 3 & \mbox{ si } &0 \leq x \leq 100 \\ \ln(x+e^x) & \mbox{ si } x>100 \end{array}\right.$$
y si queremos evaluar en $$x=-1$$ obtendremos: $$f(-1)=f_2(-1)=(-1)^2+1=1+1=2$$
El siguiente ejemplo no sería una función definida a trozos ya que los conjuntos de definición de las subfunciones no son disjuntos: $$$\displaystyle f(x)=\left\{\begin{array}{rcl} x & \mbox{ si } & x < 0 \\ x+1 & \mbox{ si } & -1 < x < 2 \\ -3 & \mbox{ si } x\geq 2 \end{array}\right.$$$
ya que para puntos en $$(-1,0)$$ se tendría que evaluar la función en $$f_1(x)=x$$ y en $$f_2(x)=x+1$$, y como obentdríamos dos valores para un solo punto, ésto no cumpliría la definición de función.
