Una funció definida a trossos és una funció l'expressió analítica de la qual no és única sinó que depèn del valor de la variable independent.
Exemple
Així la funció definida per
Per calcular la imatge d'un element
Exemple
En el cas anterior per exemple,
- si
- si
- si
- si
Com les expressions que defineixen cada un dels trossos tenen com a domini com a mínim el mateix tros, el domini de la funció
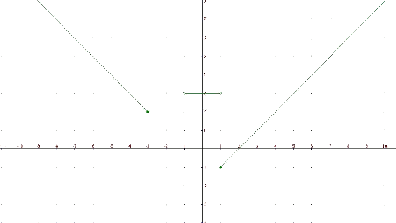
Vegem uns exemples de funcions definides a trossos:
Exemple
Considerem la funció
La seva gràfica és la unió de les gràfiques de les funcions
La representació gràfica seria:
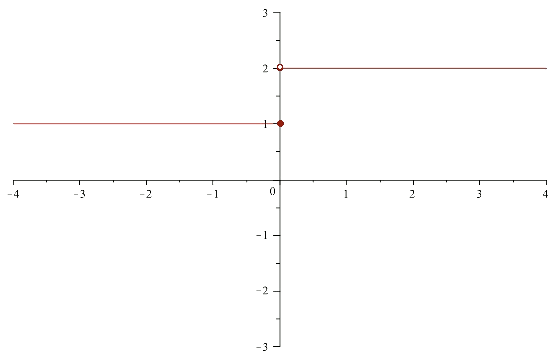
Exemple
Considerem la funció
Aquesta vegada la seva gràfica serà la unió d'una recta, una paràbola i una altra recta, definides cadascuna on indica la funció.
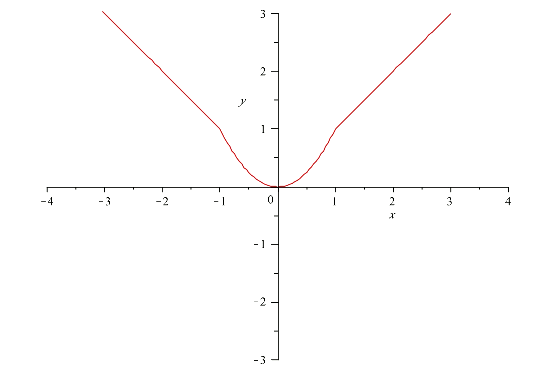
Exemple
i si volem avaluar en
Exemple
i si volem avaluar en
Exemple
El següent exemple no seria una funció definida a trossos ja que els conjunts de definició de les subfuncions no són disjunts:
ja que per punts en
