Donada una funció $$f$$ a cada element $$x$$ del domini li correspon un element $$y = f (x)$$, i per tant podem considerar el parell $$(x, y)$$ (equivalent a $$(x, f(x))$$ ).
Observeu els eixos de coordenades de la figura. Representem en l'eix d'abscisses el conjunt de valors de $$x$$ i en l'eix d'ordenades, el conjunt de valors de $$y = f(x)$$.
La gràfica d'una funció f és la representació en uns eixos de coordenades de tots els parells de la forma $$(x, f (x))$$, sent $$x$$ un element del domini de $$f$$.
A la pràctica no és possible representar tots els parells $$(x, f (x))$$, ja que en general són infinits. Per a ells s'acostumen a representar en els eixos de coordenades uns quants punts significatius i traçar la resta de la gràfica segons les propietats de la funció.
Representeu gràficament la funció $$f (x) = 2x - 4$$.
Comencem construint una taula de valors amb parells $$(x, f (x))$$:
| $$x$$ | $$f(x)$$ |
| $$-2$$ | $$f(-2)=2 \cdot (-2)-4=-8$$ |
| $$-1$$ | $$f(-1)=2 \cdot (-1)-4=-6$$ |
| $$0$$ | $$f(0)=2 \cdot (0)-4=-4$$ |
| $$1$$ | $$f(1)=2 \cdot (1)-4=-2$$ |
| $$2$$ | $$f(2)=2 \cdot (2)-4=0$$ |
Si representem els punts obtinguts:
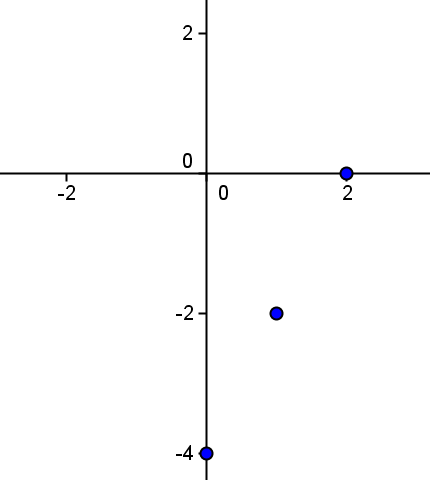
I si, finalment, els unim, obtenim la gràfica de la recta considerada:
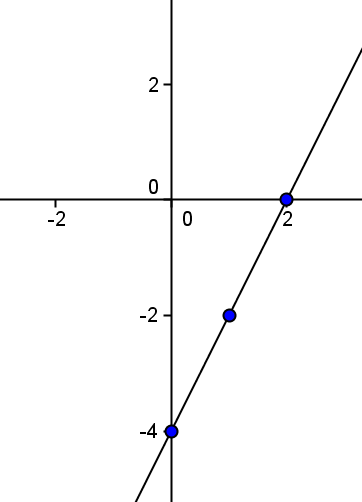
És important tenir en compte que en representar gràficament una funció no sempre s'obté un traç continu (per exemple en el cas de les funcions definides a trossos). En aquests casos cal indicar si els punts en què s'interromp el traç pertanyen o no a la gràfica de la funció. Per a això s'utilitza la següent notació:
S'acaben els traços pintant un cercle.
- Si el cercle està pintat per dins (farcit), significa que el punt pertany a la gràfica de la funció.
- Si el cercle no està pintat per dins (buit), significa que el punt no pertany a la gràfica de la funció.
Observeu la següent funció definida a trossos:
En el punt $$x = 0$$, tenim $$f (0) = 1$$.
Observem també que $$f (2)$$ no està definida, i $$f (3) = 1$$.

