Dada una función
Observad los ejes de coordenadas de la figura. Representamos en el eje de abscisas el conjunto de valores de
La gráfica de una función
En la práctica no es posible representar todos los pares
Ejemplo
Representad gráficamente la función
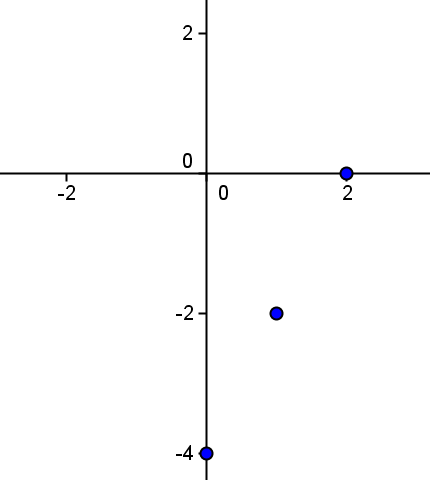
Empezamos construyendo una tabla de valores con pares
Si representamos los puntos obtenidos:
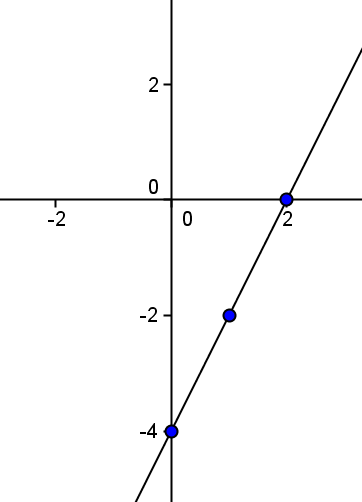
Y si por último los unimos, obtenemos la gráfica de la recta considerada:
Es importante tener en cuenta que al representar gráficamente una función no siempre se obtiene un trazo continuo (por ejemplo en el caso de las funciones definidas a trozos). En estos casos es necesario indicar si los puntos en los que se interrumpe el trazo pertenecen o no a la gráfica de la función. Para ello se utiliza la siguiente notación:
Se terminan los trazos pintando un círculo.
- si el círculo está pintado por dentro (relleno), significa que el punto pertenece a la gráfica de la función.
- si el círculo no está pintado por dentro (vacío), significa que el punto no pertenece a la gráfica de la función.
Ejemplo
Observad la siguiente función definida a trozos:
En el punto
Observamos también que

