Una función racional es una función cuya expresión analítica viene dada por un cociente entre polinomios: $$$\displaystyle f(x)=\frac{P(x)}{Q(x)}$$$ En este tipo de funciones es posible calcular la imagen de cualquier número real exceptuando aquellos que anulan el denominador, ya que al dividir entre $$0$$ no obtenemos un número real.
Por tanto podemos definir el dominio de este tipo de funciones como $$$Dom(f)=\mathbb{R}-\{x \in \mathbb{R} \mid Q(x)=0 \}$$$ Un caso destacado de función racional es la función de proporcionalidad inversa: $$\displaystyle f(x)=\frac{k}{x}$$ siendo $$k$$ una constante. Se trata de una función racional con $$P(x)=k\neq0$$ y $$Q(x)=x$$.
Su dominio es el conjunto de los números reales que no anulan el denominador, es decir, $$Dom (f) =\mathbb{R} - \{0\}$$
Su imagen es el conjunto de los números reales excepto el cero, ya que esté no es imagen de ningún elemento del dominio; es decir, $$Im (f) =\mathbb{R}- \{0\}$$
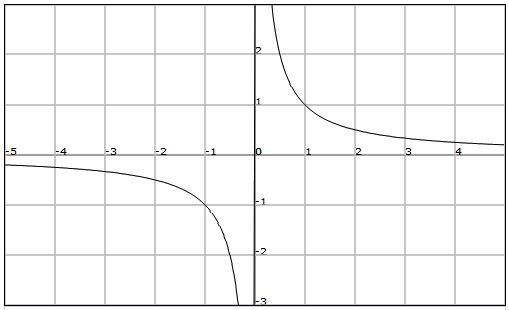
Veamos la gráfica de la función $$\displaystyle f(x)=\frac{1}{x}$$:
