Función constante, lineal y afín

Función constante

Es una función del tipo $f (x) = k$ , donde $k$ es un número real cualquiera. Fijémonos en que el valor de de $f (x)$ es siempre $k$ , independientemente del valor de $x$ .

Así, por ejemplo, si quisiésemos representar una cantidad que se mantiene constante a lo largo del tiempo $t$ , utilizaríamos una función constante $f (t) = k$ , en la que no aparece la variable $t$ .

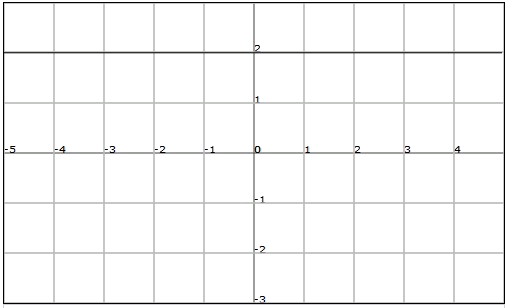
Las funciones constantes cortan el eje vertical en el valor de la constante y son paralelas al eje horizontal (y por tanto no lo cortan).

La gráfica de una función constante, por ejemplo $f (x) = 2$ , es:

imagen

Función lineal

La función de variable real que tiene por ecuación general $y = m x$ , cuya gráfica es una recta que pasa por el origen de coordenadas, se llama función lineal.

En las funciones lineales de este tipo $(y = m x)$ , el valor de m, que corresponde a un número real, se llama pendiente. El pendiente mide la inclinación de la recta respecto del eje de abscisas.

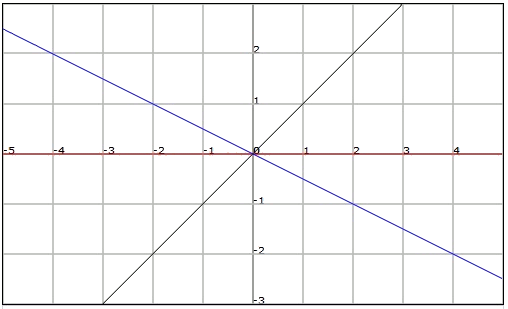
Ejemplo

El pendiente de la recta $y = - 2 x$ es $- 2$ .

El pendiente de la recta $y = 0$ es $0$ .

El pendiente de la recta $y = 3 x$ es $3$ .

Es importante entender que como mayor es el valor del pendiente $m$ , mayor inclinación respecto el eje horizontal posee la recta. Además,

Si $m$ es positivo ( $m > 0$ ), la recta pasa por el primer y por el tercer cuadrantes.
Si $m$ es negativo ( $m < 0$ ), la recta pasa por el segundo y cuarto cuadrantes.
Si $m$ es cero ( $m = 0$ ), la recta es horizontal y coincide con el eje de abscisas.

imagen

El pendiente de una recta también puede ser calculado a partir de las coordenadas de un punto de la recta para una función lineal, y de las coordenadas de dos puntos en general para una recta cualquiera.

Veamos la manera general ya que nos servirá también para las funciones afines:

Dados dos puntos de una recta (sea una función lineal o afín), $(x_{1}, y_{1})$ y $(x_{2}, y_{2})$ , podemos calcular el pendiente de dicha recta mediante la expresión: $m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$

Ejemplo

Dada la siguiente recta que pasa por el punto $(2, - 1)$ :

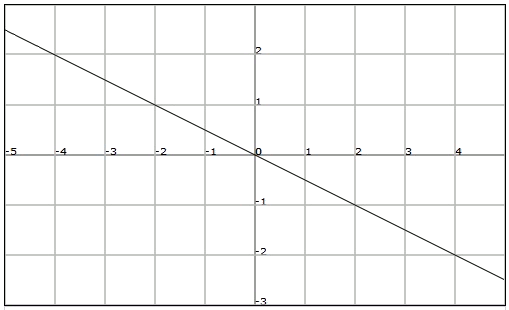
imagen

podemos calcular el pendiente, ya que además del punto $A$ , sabemos que pasa por el origen. Así, aplicando la fórmula: $m = \frac{- 1 - 0}{2 - 0} = - \frac{1}{2}$

Función afín

La función de variable real que tiene como ecuación general $y = m x + n$ , cuya gráfica es una recta que no pasa por el origen (si $n \neq 0$ ), se llama función afín.

Como en el caso anterior, $m$ es el pendiente de la recta.

Es destacable también que el punto de corte de una función afín $f (x) = m x + n$ con el eje de ordenadas es el punto $(0, n)$ .

Ejemplo

Un ejemplo de función afín podría ser $f (x) = - x + 2$

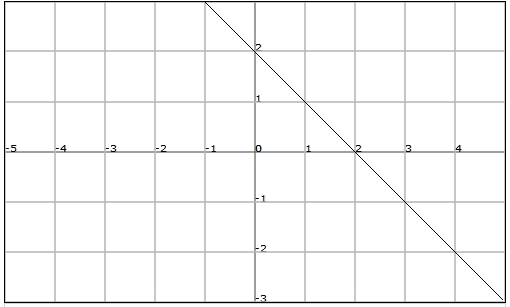
imagen

Ejemplo

Dadas las siguientes funciones, determinad de qué tipo son, en qué punto cortan el eje de ordenadas, el de abscisas, y cuál es su pendiente.

$f (x) = 2$
$f (x) = 2 x$
$f (x) = 2 x + 2$
Se trata de una función constante. Su pendiente es $0$ y por tanto es paralela al eje de abscisas. Corta el eje vertical en $(0, 2)$ .
Se trata de una función lineal. Su pendiente es $2$ . Corta ambos ejes en el punto $(0, 0)$ .
Se trata de una función afín. Su pendiente es $2$ . Corta el eje vertical en el punto $(0, 2)$ , y el eje horizontal en $(- 1, 0)$ (hacemos $y = 0 = 2 x + 2$ y resolvemos).

imagen