Funció constant
És una funció del tipus $$f(x) = k$$ on $$k$$ és un nombre real qualsevol. Fixem-nos que el valor de $$f(x)$$ és sempre $$k$$, independentment del valor de $$x$$.
Així, per exemple, si volguéssim representar una quantitat que es manté constant al llarg del temps $$t$$, utilitzaríem una funció constant $$f(t)=k$$, en què no apareix la variable $$t$$.
Les funcions constants tallen l'eix vertical en el valor de la constant i són paral·leles a l'eix horitzontal (i per tant no ho tallen).
La gràfica d'una funció constant, per exemple $$f (x) = 2$$, és:
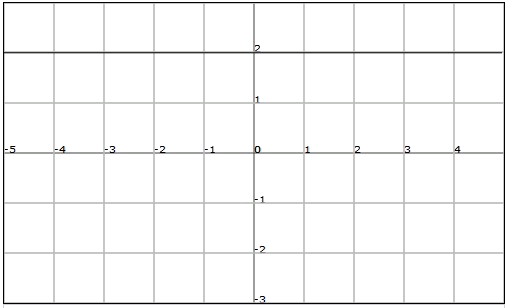
Funció lineal
La funció de variable real que té per equació general $$y = mx$$, la gràfica és una recta que passa per l'origen de coordenades, es diu funció lineal.
En les funcions lineals d'aquest tipus $$(y = mx)$$, el valor de m, que correspon a un nombre real, es diu pendent. El pendent mesura la inclinació de la recta respecte de l'eix d'abscisses.
El pendent de la recta $$y = -2x$$ és $$-2$$.
El pendent de la recta $$y = 0$$ és $$0$$.
El pendent de la recta $$y = 3x$$ és $$3$$.
És important entendre que com més gran és el valor del pendent m, major inclinació respecte l'eix horitzontal té la recta. A més,
-
Si $$m$$ és positiu ($$m> 0$$), la recta passa pel primer i pel tercer quadrants.
-
Si $$m$$ és negatiu ($$m <0$$), la recta passa pel segon i quart quadrants.
- Si $$m$$ és zero ($$m = 0$$), la recta és horitzontal i coincideix amb l'eix d'abscisses.
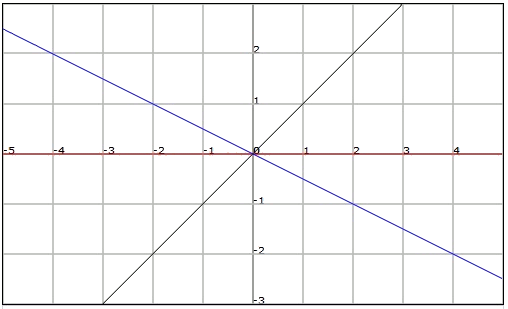
El pendent d'una recta també pot ser calculat a partir de les coordenades d'un punt de la recta per a una funció lineal, i de les coordenades de dos punts en general d'una recta qualsevol.
Vegem la manera general ja que ens servirà també per a les funcions afins:
Donats dos punts d'una recta (sigui una funció lineal o afí), $$(x_1, y_1)$$ i $$(x_2,y_2)$$, podem calcular el pendent d'aquesta recta mitjançant l'expressió: $$$\displaystyle m=\frac{y_2-y_1}{x_2-x_1}$$$
Donada la següent recta que passa pel punt $$(2,-1)$$:
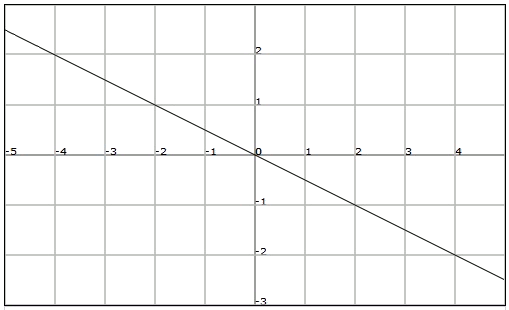
podem calcular el pendent, ja que a més del punt $$A$$, sabem que passa per l'origen. Així, aplicant la fórmula: $$$\displaystyle m=\frac{-1-0}{2-0}=-\frac{1}{2}$$$
Funció afí
La funció de variable real que té com a equació general $$y = mx + n$$, la gràfica és una recta que no passa per l'origen (si $$n\neq 0$$), s'anomena funció afí.
Com en el cas anterior, $$m$$ és el pendent de la recta.
És destacable també que el punt de tall d'una funció afí $$f(x) = mx + n$$ amb l'eix d'ordenades és el punt $$(0, n)$$.
Un exemple de funció afí podria ser $$f (x) = -x +2$$
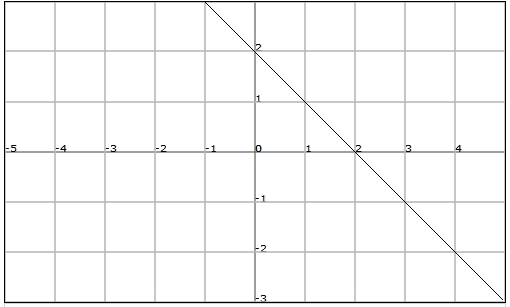
Donades les següents funcions, determineu de quin tipus són, en quin punt tallen l'eix d'ordenades, el d'abscisses, i quin és el seu pendent.
- $$f (x) = 2$$
- $$f (x) = 2x$$
-
$$f (x) = 2x +2$$
- Es tracta d'una funció constant. El seu pendent és $$0$$ i per tant és paral·lela a l'eix d'abscisses. Talla l'eix vertical en $$(0,2)$$.
- Es tracta d'una funció lineal. El seu pendent és $$2$$. Talla dos eixos en el punt $$(0,0)$$.
- Es tracta d'una funció afí. El seu pendent és $$2$$. Talla l'eix vertical en el punt $$(0, 2)$$, i l'eix horitzontal en $$(-1, 0)$$ (fem $$y = 0 = 2x + 2$$ i resolem).

