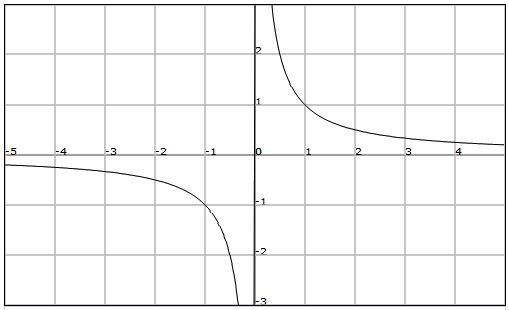
Una funció racional és una funció on l'expressió analítica ve donada per un quocient entre polinomis: $$$\displaystyle f(x)=\frac{P(x)}{Q(x)}$$$ En aquest tipus de funcions és possible calcular la imatge de qualsevol nombre real exceptuant aquells que anul·len el denominador, ja que en dividir entre $$0$$ no obtenim un nombre real.
Per tant podem definir el domini d'aquest tipus de funcions com $$$Dom(f)=\mathbb{R}-\{x \in \mathbb{R} \mid Q(x)=0 \}$$$ Un cas destacat de funció racional és la funció de proporcionalitat inversa: $$\displaystyle f(x)=\frac{k}{x}$$ sent $$k$$ una constant. Es tracta d'una funció racional amb $$P(x)=k\neq0$$ i $$Q(x)=x$$.
El seu domini és el conjunt dels nombres reals que no anul·len el denominador, és a dir, $$Dom (f) =\mathbb{R} - \{0\}$$
La seva imatge és el conjunt dels nombres reals excepte el zero, ja que aquest no és imatge de cap element del domini, és a dir, $$Im (f) =\mathbb{R}- \{0\}$$
Vegem la gràfica de la funció $$\displaystyle f(x)=\frac{1}{x}$$:
