Per representar gràficament una funció, utilitzem el sistema d'eixos cartesians en els quals figuren els valors de les 2 variables: la variable independent $$x$$ a l'eix de abscisses, i la variable dependent $$y$$ en l'eix d'ordenades.
Les representacions gràfiques poden ser de variable entera, variable racional o variable real, segons els conjunts numèrics amb els quals treballi cada funció.
El procediment a seguir per representar gràficament una funció quan disposem de la seva expressió algebraica és:
- Donada la funció $$y = f (x)$$, anem a crear una taula de valors amb diferents punts $$(x, y) = (x, f (x))$$
- Representem els punts obtinguts en uns eixos de coordenades.
- Unim els punts representats traçant així la gràfica de la funció.
Més endavant aprendrem formes més òptimes i precises de representar una funció, ja que per a casos en què la forma de la funció sigui desconeguda necessitaríem massa punts per fer-nos una idea exacta del comportament de la funció. També veurem que el nombre de punts necessaris per poder representar una funció depèn de la funció, i amb temps i pràctica s'aprèn que escollint els punts amb habilitat es necessiten menys.
Representa gràficament la funció $$\displaystyle y=\frac{x}{3}-2$$
Comencem calculant una taula de valors:
| $$x$$ | $$y = f (x)$$ |
| $$0$$ | $$\displaystyle y=\frac{0}{3}-2=-2$$ |
| $$1$$ | $$\displaystyle y=\frac{1}{3}-2=\frac{-5}{3}$$ |
| $$3$$ | $$y=\displaystyle \frac{3}{3}-2=-1$$ |
| $$6$$ | $$\displaystyle y=\frac{6}{3}-2=0$$ |
| ... | ... |
Per tant tenim els punts:
| $$x$$ | $$y$$ |
| $$0$$ | $$-2$$ |
| $$1$$ | $$\displaystyle \frac{-5}{3}$$ |
| $$3$$ | $$-1$$ |
| $$6$$ | $$0$$ |
Que podem representar en uns eixos de coordenades:
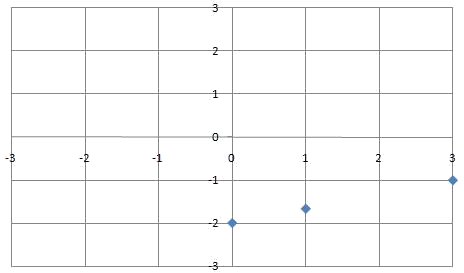
I que si unim ens donen la gràfica de la funció:
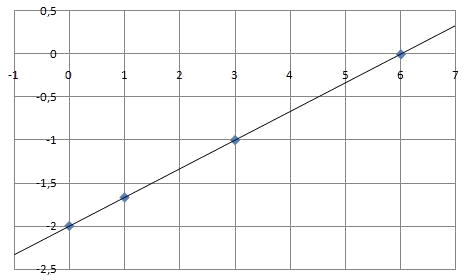
Representem ara la funció $$y=x^2+2x-3$$. Com en el cas anterior comencem calculant una taula de valors:
| $$x$$ | $$y = f (x)$$ |
| $$0$$ | $$-3$$ |
| $$1$$ | $$0$$ |
| $$-1$$ | $$-4$$ |
| $$2$$ | $$5$$ |
| $$-2$$ | $$-3$$ |
| $$-3$$ | $$0$$ |
Que podem representar gràficament:
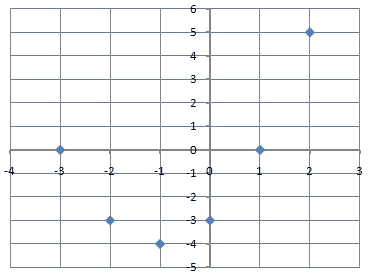
I després unir per obtenir la gràfica de la funció: