Para representar gráficamente una función, utilizamos el sistema de ejes cartesianos en los cuales figuran los valores de las 2 variables: la variable independiente $$x$$ en el eje de abscisas, y la variable dependiente $$y$$ en el eje de ordenadas.
Las representaciones gráficas pueden ser de variable entera, variable racional o variable real, según los conjuntos numéricos con los cuáles trabaje cada función.
El procedimiento a seguir para representar gráficamente una función cuando dispongamos de su expresión algebraica es:
- Dada la función $$y = f (x)$$, creamos una tabla de valores con distintos puntos $$(x, y) = (x, f (x))$$
- Representamos los puntos obtenidos en unos ejes de coordenadas.
- Unimos los puntos representados trazando así la gráfica de la función.
Más adelante aprenderemos formas más óptimas y precisas de representar una función, ya que para casos en los que la forma de la función sea desconocida necesitaríamos demasiados puntos para hacernos una idea exacta del comportamiento de la función. También veremos que el número de puntos necesarios para poder representar una función depende de la función, y con tiempo y práctica se aprende que escogiendo los puntos con habilidad se necesitan menos.
Representa gráficamente la función $$\displaystyle y=\frac{x}{3}-2$$
Empezamos calculando una tabla de valores:
| $$x$$ | $$y = f (x)$$ |
| $$0$$ | $$\displaystyle y=\frac{0}{3}-2=-2$$ |
| $$1$$ | $$\displaystyle y=\frac{1}{3}-2=\frac{-5}{3}$$ |
| $$3$$ | $$y=\displaystyle \frac{3}{3}-2=-1$$ |
| $$6$$ | $$\displaystyle y=\frac{6}{3}-2=0$$ |
| ... | ... |
Por tanto tenemos los puntos:
| $$x$$ | $$y$$ |
| $$0$$ | $$-2$$ |
| $$1$$ | $$\displaystyle \frac{-5}{3}$$ |
| $$3$$ | $$-1$$ |
| $$6$$ | $$0$$ |
Que podemos representar en unos ejes de coordenadas:
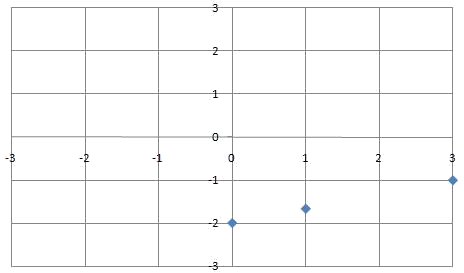
Y que si unimos nos dan la gráfica de la función:
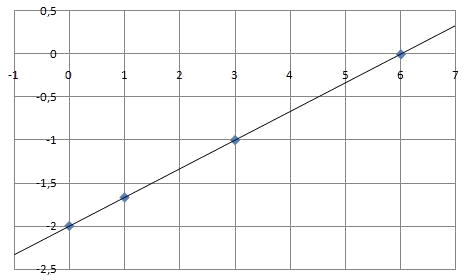
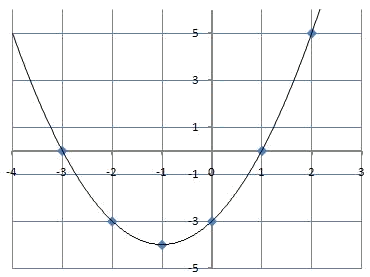
Representemos ahora la función $$y=x^2+2x-3$$. Como en el caso anterior empezamos calculando una tabla de valores:
| $$x$$ | $$y = f (x)$$ |
| $$0$$ | $$-3$$ |
| $$1$$ | $$0$$ |
| $$-1$$ | $$-4$$ |
| $$2$$ | $$5$$ |
| $$-2$$ | $$-3$$ |
| $$-3$$ | $$0$$ |
Que podemos representar gráficamente:
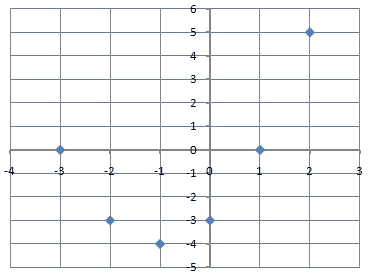
Y luego unir para obtener la gráfica de la función: