Concepto y ecuación de una función

Concepto de función

Una función es una relación entre dos conjuntos que cumple que a cada elemento del conjunto de partida se le asigna un único elemento del conjunto de llegada.

Podemos entender la función como una máquina que transforma un elemento del conjunto de salida en un elemento del conjunto de llegada.

Una forma útil de representar las funciones son los conocidos diagramas de Venn. Observamos que a cada elemento del conjunto de salida A, se le asigna un elemento del conjunto de llegada B:

f:

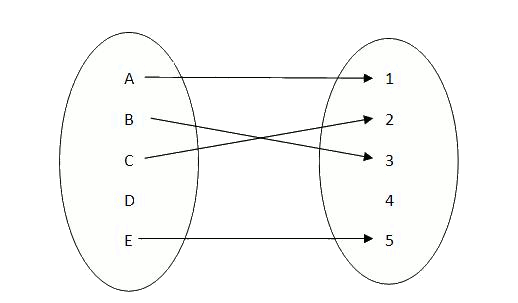
imagen

Para ver la diferencia entre lo que es una función y lo que no, podemos observar la siguiente figura

g:

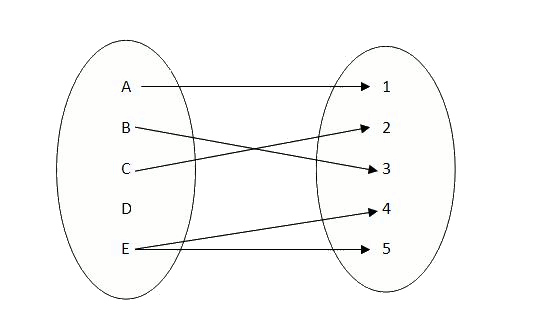
imagen

Así, mientras que la primera relación f sí que es una función ya que asigna un único elemento del conjunto de llegada a cada elemento del conjunto de partida, la relación g no es una función ya que existen elementos del conjunto de salida a los que se asigna más de un elemento del conjunto de llegada (E).

El conjunto de salida recibe el nombre de conjunto inicial, y el conjunto de llegada el nombre de conjunto final.

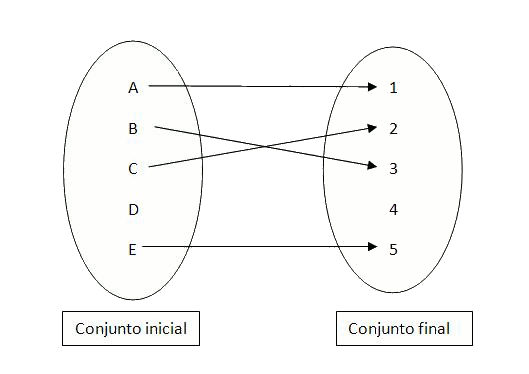
imagen

Los valores del conjunto inicial a los cuales podemos aplicar la función constituyen el dominio de la función. Los elementos del conjunto de llegada que podemos obtener aplicando la función a un elemento del dominio constituyen la imagen de la función.

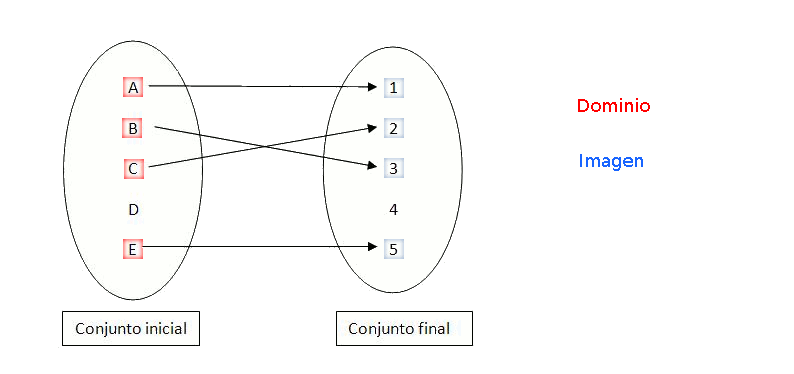
imagen

Los elementos del dominio se llaman antiimágenes, y los de la imagen, imágenes.

Ejemplo

Imaginemos que para preparar un plato de arroz en concreto ponemos tres tazas de arroz por cada dos personas más dos tazas "extra" por si alguien quiere repetir. Podemos representar esta relación de la siguiente manera:

nº de tazas de arroz=32⋅ nº de personas+2

Observamos que el conjunto inicial será el de los números naturales y que el conjunto de llegada serán fracciones positivas. Por tanto:

Conjunto inicial =N=1,2,3,4,5...

Conjunto final =Q+={12,23,25,3,72,94,103,125,…}

En esta función, el dominio coincide con el conjunto de salida. En cambio, la imagen es sólo un subconjunto de los racionales positivos. Esto se traduce en:

Dom (f)=N

Im(f)={72,5,132,8,192,11,…}

Por último si queremos saber cuántas tazas de arroz necesitamos para 10 personas en realidad lo que nos estamos preguntando es la imagen de 10, es decir, f(10):

f(10)=32⋅10+2=17

Por tanto necesitamos 17 tazas de arroz para 10 personas.

En cambio, si sabiendo que hemos puesto 15,5 tazas de arroz nos preguntamos el número de personas para el que era el arroz, lo que en realidad nos estamos preguntando es el valor de la antiimagen de 15,5, es decir, f−1(15,5): 15,5=32x+213.5=32xx=2⋅13.53=9

Por tanto el arroz era para 9 personas y f−1(15,5)=9.

Ecuación de una función

La ecuación de una función es la expresión algebraica que resume cómo se obtienen los valores del conjunto final a partir de los valores del conjunto inicial.

Ejemplo

Dada la función f definida por hacer la tercera parte y restar dos a un número entero, la ecuación de dicha función es:

f(x)=x3−2

Se llama variable independiente a los valores que pueden tomar los elementos del dominio de la función. Generalmente se denota por x. En el ejemplo anterior, x∈Z ya que así lo especifica el enunciado.

Se llama variable dependiente a los valores que pueden tomar las imágenes. Generalmente se denota por la letra y, dónde y=f(x).

Ejemplo

En el ejemplo anterior, y∈{−2,−53,−73,−43,−83,−1,…}⊂Q