Concepte de funció
Una funció és una relació entre dos conjunts que compleix que a cada element del conjunt de partida se li assigna un únic element del conjunt d'arribada.
Podem entendre la funció com una màquina que transforma un element del conjunt de sortida a un element del conjunt d'arribada.
Una manera útil de representar les funcions són els coneguts diagrames de Venn. Observem que a cada element del conjunt de sortida $$A$$, se li assigna un element del conjunt d'arribada $$B$$:
$$f:$$
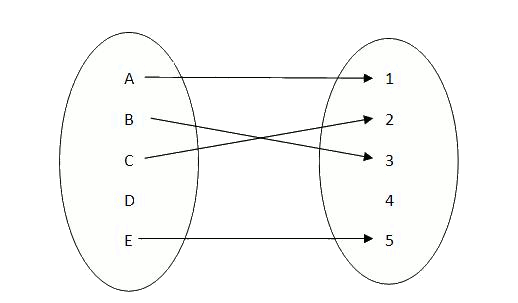
Per veure la diferència entre el que és una funció i el que no, podem observar la següent figura.
$$g:$$
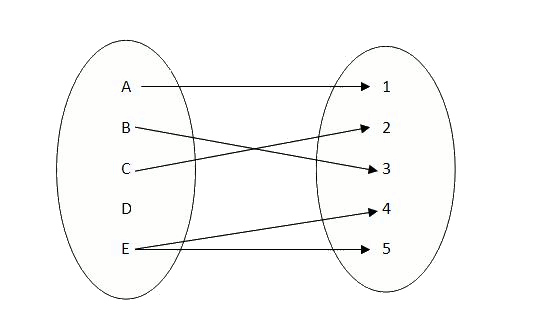
Així, mentre que la primera relació $$f$$ sí que és una funció ja que assigna un únic element del conjunt d'arribada a cada element del conjunt de partida, la relació $$g$$ no és una funció ja que existeixen elements del conjunt de sortida als quals se'ls assigna més d'un element del conjunt d'arribada (E).
El conjunt de sortida rep el nom de conjunt inicial, i el conjunt d'arribada el nom de conjunt final.
Els valors del conjunt inicial als quals podem aplicar la funció constitueixen el domini de la funció. Els elements del conjunt d'arribada que podem obtenir aplicant la funció a un element del domini constitueixen la imatge de la funció.
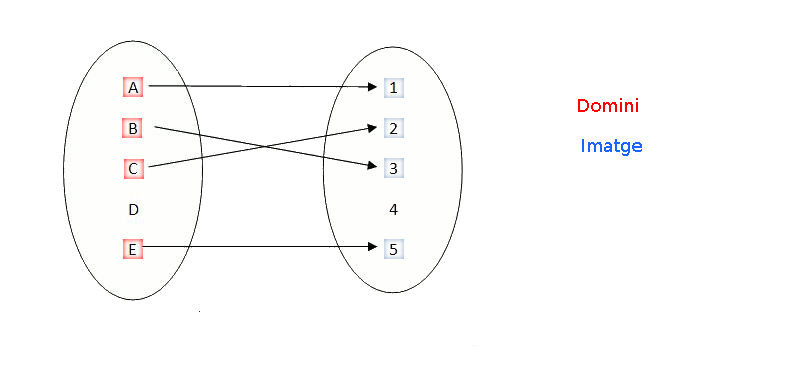
Els elements del domini es diuen antiimatges, i els de la imatge, imatges.
Imaginem que per preparar un plat d'arròs en concret posem tres tasses d'arròs per cada dues persones més dos tasses "extra" per si algú vol repetir. Podem representar aquesta relació de la següent manera:
$$$\mbox{nº de tasses d'arròs}=\displaystyle \frac{3}{2}\cdot \mbox{ nº de persones}+2$$$
Observem que el conjunt inicial serà el dels nombres naturals i que el conjunt d'arribada seran fraccions positives. Per tant:
Conjunt inicial $$=\mathbb{N} = {1, 2, 3, 4, 5...}$$
Conjunt final $$ = \mathbb{Q}^+=\Big\{ \displaystyle \frac{1}{2}, \frac{2}{3}, \frac{2}{5}, 3, \frac{7}{2}, \frac{9}{4}, \frac{10}{3}, \frac{12}{5}, \ldots\Big\}$$
En aquesta funció, el domini coincideix amb el conjunt de sortida. En canvi, la imatge és només un subconjunt dels racionals positius. Això es tradueix en:
$$Dom \ (f) = \mathbb{N}$$
$$Im (f) =\displaystyle \Big\{\frac{7}{2}, 5,\frac{13}{2},8,\frac{19}{2},11, \ldots\Big\}$$
Finalment si volem saber quantes tasses d'arròs necessitem per a $$10$$ persones en realitat el que ens estem preguntant és la imatge de $$10$$, és a dir, $$f(10)$$:
$$$f(10)=\displaystyle \frac{3}{2}\cdot 10+2=17$$$
Per tant necessitem $$17$$ tasses d'arròs per a $$10$$ persones.
En canvi, si sabent que hem posat $$15,5$$ tasses d'arròs ens preguntem el nombre de persones per al qual era l'arròs, el que en realitat ens estem preguntant és el valor de la antiimatge de $$15,5$$, és a dir, $$f^{-1}(15,5)$$: $$$\displaystyle 15,5=\frac{3}{2}x+2 \\ 13.5=\frac{3}{2}x \\ x=\displaystyle \frac{2 \cdot 13.5}{3}=9$$$
Per tant l'arròs era per $$9$$ persones i $$f^{-1}(15,5)=9$$.
Equació d'una funció
L'equació d'una funció és l'expressió algebraica que resumeix com s'obtenen els valors del conjunt final a partir dels valors del conjunt inicial.
Per exemple, donada la funció $$f$$ definida per fer la tercera part i restar dos a un nombre sencer, l'equació d'aquesta funció és:
$$$f(x)=\displaystyle \frac{x}{3}-2$$$
Es diu variable independent als valors que poden prendre els elements del domini de la funció. Generalment es denota per $$x$$.
En l'exemple anterior, $$x \in \mathbb{Z}$$ ja que així ho especifica l'enunciat.
Es diu variable dependent als valors que poden prendre les imatges. Generalment es denota per la lletra $$y$$, on $$y = f (x)$$.
En l'exemple anterior, $$$y \in \Big\{-2,\displaystyle \frac{-5}{3}, \frac{-7}{3},\frac{-4}{3},\frac{-8}{3}, -1, \ldots\Big\} \subset \mathbb{Q}$$$
