Una función irracional es una función en cuya expresión analítica la variable independiente $$x$$ aparece debajo del símbolo de raíz.
En este apartado consideraremos únicamente funciones irracionales del tipo $$$\displaystyle f(x)=\sqrt[n]{g(x)}$$$ con $$g(x)$$ una función racional.
- Si el índice $$n$$ de la raíz es impar, es posible calcular la imagen de cualquier número real, siempre y cuando la expresión $$g (x)$$ sea un número real, es decir, $$Dom(f)=Dom(g)$$.
- Si el índice $$n$$ de la raíz es par, para poder calcular imágenes necesitamos que $$g (x)$$ sea positiva o cero, ya que las raíces pares de un número negativo no son números reales. Por tanto el dominio de $$f$$ son las soluciones de la inecuación $$g(x) \geq 0$$. En otras palabras, $$Dom (f) = \{x \in \mathbb{R} \mid g(x) \geq 0\}$$.
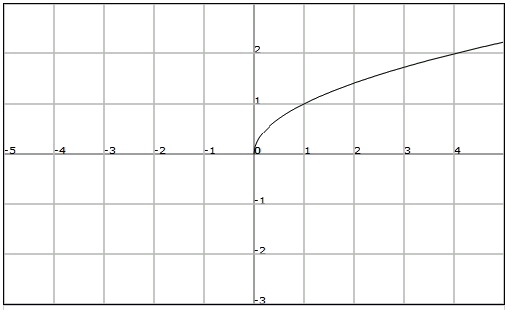
Estudiemos ahora el caso más simple de función irracional: la función raíz cuadrada $$\displaystyle f(x)=\sqrt{x}$$.
Se trata de una función en que el índice de la raíz es $$2$$. Por tanto, su dominio es el conjunto de soluciones de la inecuación $$x \geq 0$$. Así tenemos $$Dom (f) = [0, +\infty)$$ La imagen de la función raíz cuadrada es, como en el caso del dominio, el conjunto de los reales mayores o igual que cero, $$Im (f) = [0, +\infty)$$
Veamos su representación gráfica:
