An irrational function is a function whose analytic expression has the independent variable $$x$$ under the root symbol.
In this paragraph we will consider only irrational functions of the type $$$\displaystyle f(x)=\sqrt[n]{g(x)}$$$ with $$g(x)$$ a rational function.
- If the index $$n$$ of the root is odd, it is possible to calculate the image of any real number, if the expression $$g (x)$$ is a real number, that is $$Dom(f)=Dom(g)$$.
- If the index $$n$$ of the root is a even, to be able to calculate images we need $$g (x)$$ to be positive or zero, since the even roots of a negative number are not real numbers. Therefore the domain of $$f$$ are the solutions of the inequation $$g(x) \geq 0$$. In other words, $$Dom (f) = \{x \in \mathbb{R} \mid g(x) \geq 0\}$$.
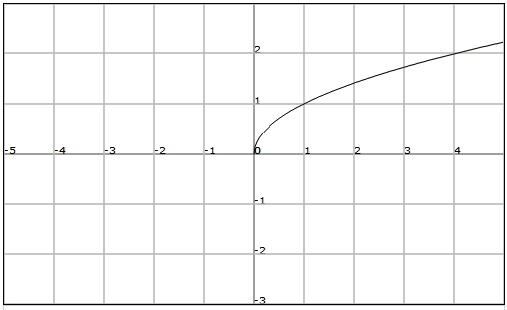
Let's study now the simplest case of irrational function: the square root function $$\displaystyle f(x)=\sqrt{x}$$.
This is a function in which the index of the root is $$2$$. Therefore, its domain is the set of solutions of the inequation $$x \geq 0$$. Thus we have $$Dom (f) = [0, +\infty)$$ The image of the square root function is, as is the case of the domain, the set of the positive numbers, $$Im (f) = [0, +\infty)$$
Let's see its graphic representation: