Una funció irracional és una funció on en l'expressió analítica la variable independent $$x$$ apareix dins del símbol de l'arrel.
En aquest apartat considerarem únicament funcions irracionals del tipus $$$\displaystyle f(x)=\sqrt[n]{g(x)}$$$ amb $$g(x)$$ una funció racional.
- Si l'índex $$n$$ de l'arrel és senar, és possible calcular la imatge de qualsevol nombre real, sempre i quan l'expressió g(x) sigui un nombre real, és a dir, $$Dom(f)=Dom(g)$$.
- Si l'índex $$n$$ de l'arrel és parell, per poder calcular imatges necessitem que $$g (x)$$ sigui positiva o zero, ja que les arrels parells d'un nombre negatiu no són nombres reals. Per tant el domini de $$f$$ són les solucions de la inequació $$g(x) \geq 0$$. En altres paraules, $$Dom (f) = \{x \in \mathbb{R} \mid g(x) \geq 0\}$$.
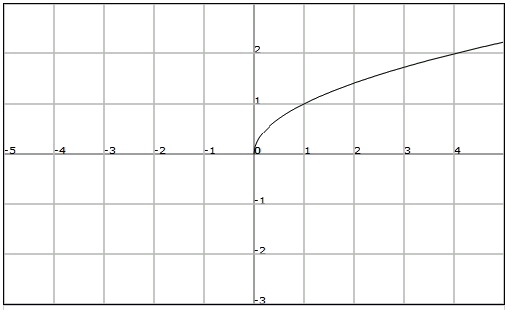
Estudiem ara el cas més simple de funció irracional: la funció arrel quadrada $$\displaystyle f(x)=\sqrt{x}$$.
Es tracta d'una funció en què l'índex de l'arrel és $$2$$. Per tant, el seu domini és el conjunt de solucions de la inequació $$x \geq 0$$. Així tenim $$Dom (f) = [0, +\infty)$$ La imatge de la funció arrel quadrada és, com en el cas del domini, el conjunt dels reals més grans o igual que zero, $$Im (f) = [0, +\infty)$$
Vegem la seva representació gràfica:
