La funció que assigna a la variable independent
Així, per exemple, les funcions
En particular, la funció exponencial de base
Gràfica
La gràfica de la funció exponencial varia segons si la base
Vegem a continuació les gràfiques de
És destacable que la gràfica d'una funció exponencial sempre passa pel punt
Exemple
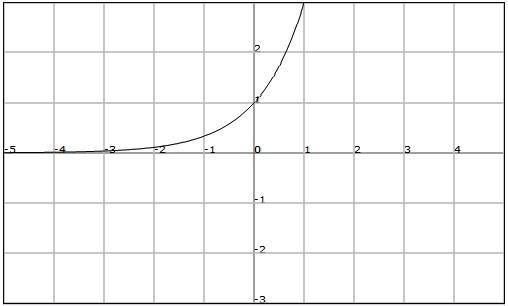
Exemple
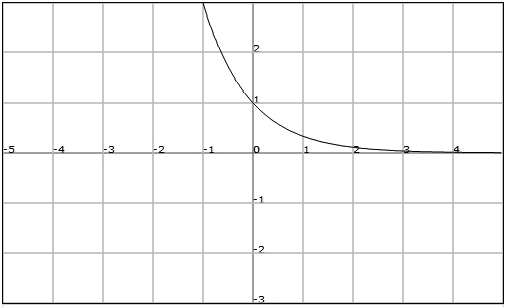
Propietats
A partir de la seva representació gràfica observem que les funcions exponencials compleixen les propietats següents:
- Domini:
- Imatge:
- Cotes:acotada inferiorment per
- Intersecció amb els eixos: Talla amb l'eix vertical en
- Continuïtat: És contínua en tot
- Asímptotes: La recta
- Periodicitat:No és periòdica.
- Simetries: No és simètrica.
- Monotonia: Si
- Extrems relatius: No en té.
- Injectivitat i exhaustivitat: És injectiva (les imatges de punts diferents són diferents), però no és exhaustiva ja que la imatge no és tot
