La función que asigna a la variable independiente $$x$$ el valor de $$f(x)=a^x$$ se llama función exponencial de base $$a$$, donde $$a$$ es un número real positivo distinto de $$1$$.
Así, por ejemplo, las funciones $$f(x)=3^x$$ y $$h(x)=0.8^x$$ son funciones exponenciales de base $$3$$ y $$0.8$$ respectivamente.
En particular, la función exponencial de base $$e$$, $$f(x)=e^x$$, es especialmente importante ya que describe el comportamiento de varias situaciones reales: evolución de poblaciones, desintegración radioactiva,...
Gráfica
La gráfica de la función exponencial varía según si la base $$a$$ es mayor o menor que $$1$$ (recordemos que siempre ha de ser mayor que cero y que no puede ser $$1$$).
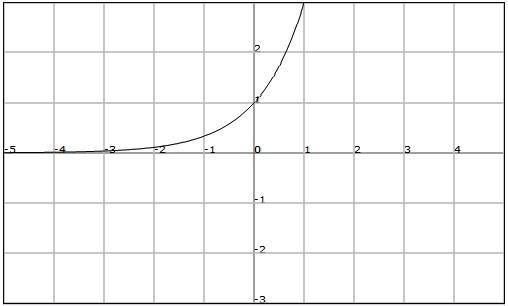
Veamos a continuación las gráficas de $$f(x)=3^x$$ y $$h(x)=\displaystyle \Big(\frac{1}{3}\Big)^x$$ para ilustrar este fenómeno.
Es destacable que la gráfica de una función exponencial siempre pasa por el punto $$(0, 1)$$.
$$f(x)=3^x$$
$$f(x)=\displaystyle \Big(\frac{1}{3}\Big)^x$$
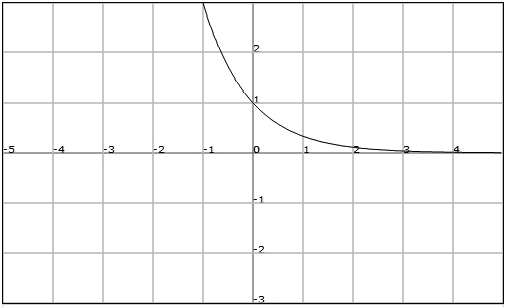
Propiedades
A partir de su representación gráfica observamos que las funciones exponenciales cumplen las propiedades siguientes:
- Dominio: $$Dom (f) = \mathbb{R}$$
- Imagen: $$Im (f) = (0, +\infty)$$
- Cotas:acotada inferiormente por $$0$$
- Intersección con los ejes:Corta con el eje vertical en $$y = 1$$. No corta el eje horizontal.
- Continuidad:Es continua en todo $$\mathbb{R}$$
- Asíntotas:La recta $$y = 0$$ es una asíntota horizontal (pero sólo en un extremo)
- Periodicidad:No es periódica.
- Simetrías: No es simétrica.
- Monotonía: Si $$a> 1$$, la función es estrictamente creciente. Si $$a <1$$, la función es estrictamente decreciente.
- Extremos relativos:No tiene.
- Inyectividad y exhaustividad: Es inyectiva (las imágenes de puntos diferentes son diferentes), pero no es exhaustiva ya que la imagen no es todo $$\mathbb{R}$$
