The function that assigns to the independent variable $$x$$ the value of $$f(x)=a^x$$ is called an exponential function of base $$a$$, where $$a$$ is a positive real number other than $$1$$.
For example, the functions $$f(x)=3^x$$ and $$h(x)=0.8^x$$ are exponential functions of base $$3$$ and $$0.8$$ respectively.
In particular, the exponential function of base $$e$$, $$f(x)=e^x$$, is especially important since it describes the behaviour of several real situations: evolution of populations, radioactive disintegration...
Graph
The graph of the exponential function changes if its base is greater or smaller than $$1$$ (let's remember that it has always to be greater than zero and that it cannot be $$1$$).
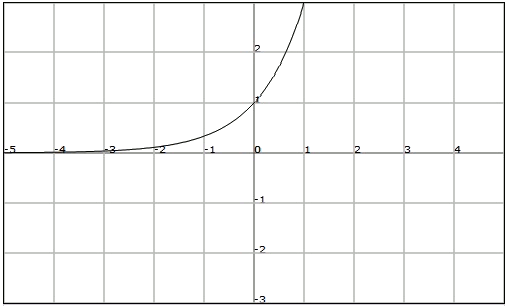
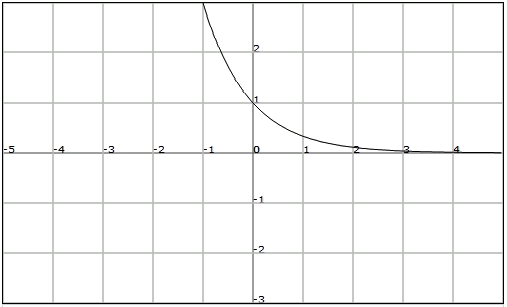
Let's see next the graphs of $$f(x)=3^x$$ and $$h(x)=\displaystyle \Big(\frac{1}{3}\Big)^x$$ to illustrate it graphically.
It is worth mentioning that the graph of an exponential function always goes through the point $$(0, 1)$$.
$$f(x)=3^x$$
$$f(x)=\displaystyle \Big(\frac{1}{3}\Big)^x$$
Properties
From its graphic representation we observe that the exponential functions satisfies the following properties:
- Domain: $$Dom (f) = \mathbb{R}$$
- Image: $$Im (f) = (0, +\infty)$$
- Bounds: bounded from below by $$0$$
- Intersection with the axes: It cuts with the vertical axis at $$y= 1$$. It does not cut the horizontal axis.
- Continuity: It is continuous in $$\mathbb{R}$$
- Asimptotes: The straight line $$y= 0$$ is a horizontal asimptote (but only in one of the extremes)
- Regularity: It is not periodic.
- Symmetries: It is not symmetric.
- Monotonicity: If $$a> 1$$, the function is strictly increasing. If $$a <1$$, the function is strictly decreasing.
- Relative extrema: It does not have any.
- Injectivity and exhaustivity: It is injective (the images of different points are different), but it is not exhaustive since the image is not $$\mathbb{R}$$
