Equation of the circumference I: reduced equation

We will call the circumference: the geometric locus of points on the plane that are equidistant to a fixed point called center. This distance is named radius.

This property is the key to finding the analytical expression of a circumference.

Let's see it:

A circumference of center $C = (a, b)$ and radius $r$ , is formed by all the points $P = (x, y)$ whose distance to the center is $r$ .

Expressing this in a mathematical equation we have: $d (C, P) = d ((a, b), (x, y)) = \sqrt{(x - a)^{2} + (y - b)^{2}} = r$ Squaring this equation we obtain the reduced equation of the circumference: $d (C, P)^{2} = (\sqrt{(x - a)^{2} + (y - b)^{2}})^{2} = (x - a)^{2} + (y - b)^{2} = r^{2}$ For which reason, any expression of the type $(x - a)^{2} + (y - b)^{2} = r^{2}$ is a circumference of radius $r$ and center at the point $(a, b)$ .

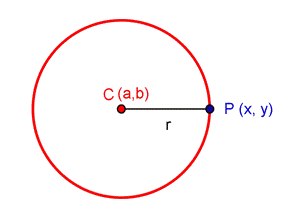
imagen

Example

$(x - 1)^{2} + (y - 2)^{2} = 3^{2}$ is a circumference of radius $3$ and centred at the point $(1, 2)$ .

When we consider a circumference centred on the origin, we are taking $C = (0, 0)$ and therefore the equation is $x^{2} + y^{2} = r^{2}$ .

Example

$x^{2} + y^{2} = 4^{2}$ it is centred on the origin and has a radius of $4$ .

The circumference with center in the origin and radius $1$ is called a unit circumference.

Example

If, for example, we want to write the equation of a circumference centred at point $(- 8, 0)$ and with diameter $36$ , the procedure is:

We calculate the radius: $r = \frac{diameter}{2} = \frac{36}{2} = 18$

We replace the parameters in the equation of the circumference, with $r = 18$ and $C = (- 8, 0)$ : $(x - (- 8)^{2}) + (y - 0)^{2} = 18^{2} \Rightarrow (x + 8)^{2} + y^{2} = 18^{2}$ So we already have the equation.