Equació de la circumferència I: equació reduïda

S'anomena circumferència al lloc geomètric dels punts del pla que equidisten d'un punt fix anomenat centre. A la distància se l'anomena radi.

Aquesta propietat és la clau per trobar l'expressió analítica d'una circumferència.

Vegem com:

Una circumferència de centre $C = (a, b)$ i radi $r$ , està formada per tots els punts $P = (x, y)$ la distància al centre és $r$ .

Expressant això en forma d'equació matemàtica tenim: $d (C, P) = d ((a, b), (x, y)) = \sqrt{(x - a)^{2} + (y - b)^{2}} = r$ Elevant al quadrat aquesta equació obtenim l'equació reduïda de la circumferència: $d (C, P)^{2} = (\sqrt{(x - a)^{2} + (y - b)^{2}})^{2} = (x - a)^{2} + (y - b)^{2} = r^{2}$ Pel que qualsevol expressió del tipus $(x - a)^{2} + (y - b)^{2} = r^{2}$ és una circumferència de radi $r$ i centre el punt $(a, b)$ .

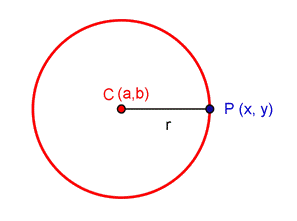
imagen

Exemple

$(x - 1)^{2} + (y - 2)^{2} = 3^{2}$ és una circumferència de radi $3$ i centrada en el punt $(1, 2)$ .

Quan considerem una circumferència centrada en l'origen, estem agafant $C = (0, 0)$ i per tant l'equació és $x^{2} + y^{2} = r^{2}$ .

Exemple

$x^{2} + y^{2} = 4^{2}$ stà centrada en l'origen i té radi $4$ .

La circumferència amb centre en l'origen i radi 1 s'anomena circumferència unitat.

Exemple

Si per exemple volem escriure l'equació d'una circumferència centrada en el punt $(- 8, 0)$ i amb diàmetre $36$ , el procediment és:

Calculem el radi: $r = \frac{diameter}{2} = \frac{36}{2} = 18$

Substituïm els paràmetres en l'equació de la circumferència, amb $r = 18$ i $C = (- 8, 0)$ : $(x - (- 8)^{2}) + (y - 0)^{2} = 18^{2} \Rightarrow (x + 8)^{2} + y^{2} = 18^{2}$ I ja tenim l'equació.