Anem a estudiar les posicions relatives en què poden trobar-se en un mateix pla una recta i una circumferència.
Per això donarem nom a diversos punts, rectes i segments que són singulars en la circumferència:
- Centre, és un punt interior equidistant de tots els punts de la circumferència.
- Radi, és la distància des del centre a un punt de la circumferència.
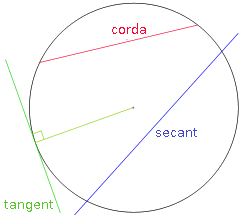
- Corda, és el segment que uneix dos punts de la circumferència; les cordes de longitud màxima són els diàmetres.
- Recta secant és la que talla la circumferència en dos punts.
- Recta tangent és la que toca a la circumferència en un sol punt.
- Punt de tangència, és el punt de contacte de la tangent amb la circumferència.
Per trobar els punts comuns a una circumferència i una recta resoldrem el sistema format per les equacions de les dues. És a dir, si tenim:
- la circumferència donada per l'equació $$(x-a)^2+(y-b)^2=r^2$$ o bé per l'equació $$x^2+y^2+Ax+By+C=0$$
- la recta donada per l'equació general d'una recta: $$y-y_0=m \cdot (x-x_0)$$
El que hem de resoldre és un dels dos sistemes següents (depenent de com ens vingui donada la circumferència): $$$\left\{{\begin{array}{l} {(x-a)^2+(y-b)^2=r^2} \\ {y-y_0=m \cdot (x-x_0)}\end{array}}\right. \mbox{ or } \left\{{\begin{array}{l} {x^2+y^2+Ax+By+C=0} \\ {y-y_0=m \cdot (x-x_0)}\end{array}}\right.$$$
Atès que si es té l'equació reduïda de la circumferència desenvolupant els quadrats s'aconsegueix l'equació general, sempre sabrem plantejar el problema de manera que el sistema a resoldre sigui: $$$\left\{{\begin{array}{l} {x^2+y^2+Ax+By+C=0} \\ {y-y_0=m \cdot (x-x_0)}\end{array}}\right.$$$ Aïllant per exemple la $$y$$ en l'equació de la recta obtenim: $$$y=y_0+m \cdot(x-x_0)$$$ i substituint aquesta expressió en l'equació general de la circumferència obtenim: $$$x^2+(y_0+m \cdot (x-x_0))^2+Ax+B(y_0+m \cdot (x-x_0))+C=0$$$ que si ajuntem oportunament ens dóna: $$$\begin{array}{l} x^2+(y_0+m \cdot (x-x_0))^2+Ax+B(y_0+m \cdot (x-x_0))+C=0 \\ x^2+y_0^2+2\cdot y_0 \cdot m \cdot x -2 \cdot y_0 \cdot m \cdot x_0+m^2\cdot (x-x_0)^2+ \\ \ \ \ +Ax+By_0+B \cdot m \cdot x - B \cdot m \cdot x_0+C=0 \\ x^2+m^2 \cdot x^2+2 \cdot y_0 \cdot m \cdot x-2 \cdot m^2 \cdot x \cdot x_0+Ax +B \cdot m \cdot x+ \\ \ \ \ +y_0^2 -2 \cdot y_0 \cdot m \cdot x_0 + B \cdot y_0 - B \cdot m \cdot x_0 + m^2 \cdot x_0^2 +C=0 \\ x^2(1+m^2)+x(2 \cdot y_0 \cdot m-2 \cdot m^2 \cdot x_0 +A+B \cdot m)+\\ \ \ \ +y_0^2 -2 \cdot y_0 \cdot m \cdot x_0 + B \cdot m \cdot x_0 +m^2 \cdot x_0^2 + C=0 \end{array}$$$
que és una equació de segon grau en la variable $$x$$.
Atès que en general s'obté un equació de segon grau, aquesta tindrà, depenent del signe del discriminant ($$\Delta=b^2-4ac$$), les següents solucions:
- Si $$\Delta> 0$$ Dues solucions: llavors la recta i la circumferència són secants.
- Si $$\Delta = 0$$ Una solució: llavors la recta i la circumferència són tangents.
- Si $$\Delta <0$$ Cap solució: llavors la recta i la circumferència són exteriors. Per tant no es toquen en cap punt.
Vegeu en el següent dibuix algunes de les possibilitats:



