We are going to study the relative positions where a straight line and a circumference can be in the same plane.
To do so, we will name several points, straight lines and segments that are singular in the circumference:
- Center is an interior point equidistant from all the points of the circumference.
- Radius is the distance from the center to any point of the circumference.
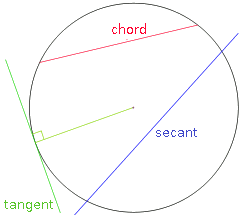
- Chord is the segment that joins two points of the circumference; the chords of maximum length are the diameters.
- Secant straight line is any line that cuts the circumference in two points.
- Tangent straight line is any line that touches the circumference at only one point.
- Touching point is the point where the tangent touches the circumference.
To find the common points of a circumference and a straight line we will solve the system formed by their equations. Namely if we have:
- the circumference given by the equation $$(x-a)^2+(y-b)^2=r^2$$ or by the equation $$x^2+y^2+Ax+By+C=0$$
- the straight line given by the general equation of a straight line: $$y-y_0=m \cdot (x-x_0)$$
What we must solve is one of two following systems (depending on the circumference given to us): $$$\left\{{\begin{array}{l} {(x-a)^2+(y-b)^2=r^2} \\ {y-y_0=m \cdot (x-x_0)}\end{array}}\right. \mbox{ or } \left\{{\begin{array}{l} {x^2+y^2+Ax+By+C=0} \\ {y-y_0=m \cdot (x-x_0)}\end{array}}\right.$$$
Note that once we know one of the two equations that define a circumference we can obtain the other one. Thus, we can consider the case: $$$\left\{{\begin{array}{l} {x^2+y^2+Ax+By+C=0} \\ {y-y_0=m \cdot (x-x_0)}\end{array}}\right.$$$ Isolating $$y$$ from the straight line we obtain: $$$y=y_0+m \cdot(x-x_0)$$$ and replacing this expression in the general equation of the circumference we obtain: $$$x^2+(y_0+m \cdot (x-x_0))^2+Ax+B(y_0+m \cdot (x-x_0))+C=0$$$ Manipulating the equation we will obtain: $$$\begin{array}{l} x^2+(y_0+m \cdot (x-x_0))^2+Ax+B(y_0+m \cdot (x-x_0))+C=0 \\ x^2+y_0^2+2\cdot y_0 \cdot m \cdot x -2 \cdot y_0 \cdot m \cdot x_0+m^2\cdot (x-x_0)^2+ \\ \ \ \ +Ax+By_0+B \cdot m \cdot x - B \cdot m \cdot x_0+C=0 \\ x^2+m^2 \cdot x^2+2 \cdot y_0 \cdot m \cdot x-2 \cdot m^2 \cdot x \cdot x_0+Ax +B \cdot m \cdot x+ \\ \ \ \ +y_0^2 -2 \cdot y_0 \cdot m \cdot x_0 + B \cdot y_0 - B \cdot m \cdot x_0 + m^2 \cdot x_0^2 +C=0 \\ x^2(1+m^2)+x(2 \cdot y_0 \cdot m-2 \cdot m^2 \cdot x_0 +A+B \cdot m)+\\ \ \ \ +y_0^2 -2 \cdot y_0 \cdot m \cdot x_0 + B \cdot m \cdot x_0 +m^2 \cdot x_0^2 + C=0 \end{array}$$$
which is an equation of the second grade in the variable $$x$$.
Since we have a general equation of the second degree, we know that depending on the sign of the discriminant ($$\Delta=b^2-4ac$$), we will have the following solutions:
- If $$\Delta> 0$$ we have two solutions: then the straight line and the circumference are secant.
- If $$\Delta = 0$$ we only have one solution: then the straight line and the circumference are tangent.
- If $$\Delta <0$$ we have no solution: then the straight line and the circumference are exterior. Therefore they do not meet at any point.
The different possibilities can be seen in the following picture:
