Vamos a estudiar las posiciones relativas en que pueden encontrarse en un mismo plano una recta y una circunferencia.
Para ello daremos nombre a varios puntos, rectas y segmentos que son singulares en la circunferencia:
- Centro, es un punto interior equidistante de todos los puntos de la circunferencia.
- Radio, es la distancia desde el centro a un punto de la circunferencia.
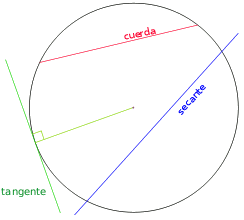
- Cuerda, es el segmento que une dos puntos de la circunferencia; las cuerdas de longitud máxima son los diámetros.
- Recta secante, es la que corta a la circunferencia en dos puntos.
- Recta tangente, es la que toca a la circunferencia en un sólo punto.
- Punto de tangencia, es el de contacto de la tangente con la circunferencia.
Para hallar los puntos comunes a una circunferencia y una recta resolveremos el sistema formado por las ecuaciones de ambas. Es decir, si tenemos:
- la circunferencia dada por la ecuación $$(x-a)^2+(y-b)^2=r^2$$ o bien por la ecuación $$x^2+y^2+Ax+By+C=0$$
- la recta dada por la ecuación general de una recta: $$y-y_0=m \cdot (x-x_0)$$
Lo que debemos resolver es uno de los dos sistemas siguientes (dependiendo de como nos venga dada la circunferencia): $$$\left\{{\begin{array}{l} {(x-a)^2+(y-b)^2=r^2} \\ {y-y_0=m \cdot (x-x_0)}\end{array}}\right. \mbox{ or } \left\{{\begin{array}{l} {x^2+y^2+Ax+By+C=0} \\ {y-y_0=m \cdot (x-x_0)}\end{array}}\right.$$$
Dado que si se tiene la ecuación reducida de la circunferencia desarrollando los cuadrados se consigue la ecuación general, siempre sabemos plantear el problema de manera que el sistema a resolver será: $$$\left\{{\begin{array}{l} {x^2+y^2+Ax+By+C=0} \\ {y-y_0=m \cdot (x-x_0)}\end{array}}\right.$$$ Aislando por ejemplo la $$y$$ en la ecuación de la recta obtenemos: $$$y=y_0+m \cdot(x-x_0)$$$ y sustituyendo esta expresión en la ecuación general de la circunferencia obtenemos: $$$x^2+(y_0+m \cdot (x-x_0))^2+Ax+B(y_0+m \cdot (x-x_0))+C=0$$$ que si juntamos oportunamente nos da: $$$\begin{array}{l} x^2+(y_0+m \cdot (x-x_0))^2+Ax+B(y_0+m \cdot (x-x_0))+C=0 \\ x^2+y_0^2+2\cdot y_0 \cdot m \cdot x -2 \cdot y_0 \cdot m \cdot x_0+m^2\cdot (x-x_0)^2+ \\ \ \ \ +Ax+By_0+B \cdot m \cdot x - B \cdot m \cdot x_0+C=0 \\ x^2+m^2 \cdot x^2+2 \cdot y_0 \cdot m \cdot x-2 \cdot m^2 \cdot x \cdot x_0+Ax +B \cdot m \cdot x+ \\ \ \ \ +y_0^2 -2 \cdot y_0 \cdot m \cdot x_0 + B \cdot y_0 - B \cdot m \cdot x_0 + m^2 \cdot x_0^2 +C=0 \\ x^2(1+m^2)+x(2 \cdot y_0 \cdot m-2 \cdot m^2 \cdot x_0 +A+B \cdot m)+\\ \ \ \ +y_0^2 -2 \cdot y_0 \cdot m \cdot x_0 + B \cdot m \cdot x_0 +m^2 \cdot x_0^2 + C=0 \end{array}$$$
que es una ecuación de segundo grado en la variable $$x$$.
Dado que en general se obtiene un ecuación de segundo grado, ésta tendrá, dependiendo del signo del discriminante ($$\Delta=b^2-4ac$$), las siguientes soluciones:
- Si $$\Delta> 0$$ Dos soluciones: entonces la recta y la circunferencia son secantes.
- Si $$\Delta = 0$$ Una solución: entonces la recta y la circunferencia son tangentes.
- Si $$\Delta <0$$ Ninguna solución: entonces la recta y la circunferencia son exteriores. Por lo tanto no se juntan en ningún punto.
Véanse en el siguiente dibujo algunas de las posibilidades:



