Ecuación de la circunferencia I: ecuación reducida

Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. A la distancia se le denomina radio.

Esta propiedad es la clave para hallar la expresión analítica de una circunferencia.

Veamos como:

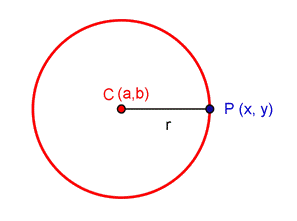
Una circunferencia de centro $C = (a, b)$ y radio $r$ , está formada por todos los puntos $P = (x, y)$ cuya distancia al centro es $r$ .

Expresando esto en forma de ecuación matemática tenemos: $d (C, P) = d ((a, b), (x, y)) = \sqrt{(x - a)^{2} + (y - b)^{2}} = r$ Elevando al cuadrado esta ecuación obtenemos la ecuación reducida de la circunferencia: $d (C, P)^{2} = (\sqrt{(x - a)^{2} + (y - b)^{2}})^{2} = (x - a)^{2} + (y - b)^{2} = r^{2}$ Por lo que cualquier expresión del tipo $(x - a)^{2} + (y - b)^{2} = r^{2}$ es una circunferencia de radio $r$ y centro el punto $(a, b)$ .

imagen

Ejemplo

$(x - 1)^{2} + (y - 2)^{2} = 3^{2}$ es una circunferencia de radio $3$ y centrada en el punto $(1, 2)$ .

Cuando consideramos una circunferencia centrada en el origen, estamos cogiendo $C = (0, 0)$ y por lo tanto la ecuación es $x^{2} + y^{2} = r^{2}$ .

Ejemplo

$x^{2} + y^{2} = 4^{2}$ está centrada en el origen y tiene radio $4$ .

La circunferencia con centro en el origen y radio 1 se llama circunferencia unidad.

Ejemplo

Si por ejemplo queremos escribir la ecuación de una circunferencia centrada en el punto $(- 8, 0)$ y con diámetro $36$ , el procedimiento es:

Calculamos el radio: $r = \frac{diameter}{2} = \frac{36}{2} = 18$

Sustituimos los parámetros en la ecuación de la circunferencia, con $r = 18$ y $C = (- 8, 0)$ : $(x - (- 8)^{2}) + (y - 0)^{2} = 18^{2} \Rightarrow (x + 8)^{2} + y^{2} = 18^{2}$ Y ya tenemos la ecuación.