A fixed vector $$\overrightarrow{AB}$$ is a segment determined by the origin $$A$$ and the end $$B$$.
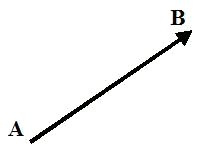
The main characteristics of a fixed vector $$\overrightarrow{AB}$$ are the following ones:
- Angle of a fixed vector $$\overrightarrow{AB}$$: it is determined by the straight line that contains $$\overrightarrow{AB}$$ and all its parallels.
- Direction of a fixed vector $$\overrightarrow{AB}$$: It determines what is the origin and what is the end of a given vector.
- Magnitude of a fixed vector $$\overrightarrow{AB}$$: it is the length of the segment $$AB$$. It is represented by $$|\overrightarrow{AB}|$$ and it is always a positive number or zero.
For example, there is a one-way street. This street may even have two lanes, but both lanes can only travel in one direction.
Classes of vectors
Two vectors are equivalent when they have equal magnitude, angle and direction.
The vectors represented in the following figure are equivalent.
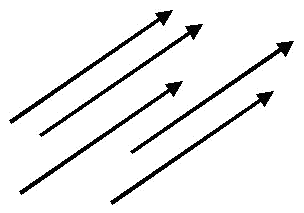
The set of all the equivalent vectors to a given vector $$\overrightarrow{AB}$$, is called a free vector. That is, the free vectors have the same magnitude, angle and direction.
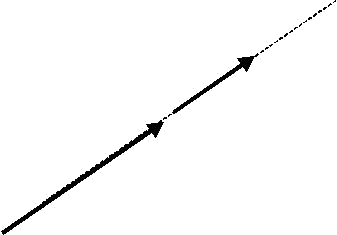
Connected vectors are equivalent vectors that exist in the same straight line. Namely, there are the fixed vectors that have the same magnitude, angle and direction, and are in the same straight line.
The inverse vectors have the same magnitude and angle, but different direction.
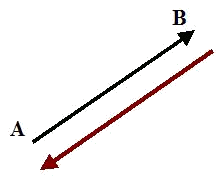
$$\vec{u}$$ and $$-\vec{u}$$ are inverse vectors since they have the same magnitude and angle, but different direction.
The unit vectors are those which magnitude is $$1$$, that is $$|\vec{u}|=1$$.
How to determine a vector
Knowing the coordinates of the origin $$A$$, and of the ending point $$B$$, we can determine the components of the vector $$\overrightarrow{AB}$$ connecting $$A$$ and $$B$$, by substracting the coordinates of the origin from those of the end: $$$ \overrightarrow{AB}= (x_2,y_2)-(x_1,y_1)=(x_2-x_1, y_2-y_1)$$$ Where $$A$$ is the point $$(x_1,y_1)$$ and $$B$$ the point $$(x_2,y_2)$$.
If $$A=(3, -1)$$ and $$B=(5,2)$$, the components of the vector $$\overrightarrow{AB}$$ are: $$(5,2)-(3,-1)=(5-3,2-(-1))=(2,3)$$.
Remember that in this case $$A$$ is the origin and $$B$$ is the end of the vector $$\overrightarrow{AB}$$.
How to compute the magnitude of a vector
1) Using its components. If we have the vector $$\vec{u}=(u_1,u_2)$$, then the magnitude of $$\vec{u}$$ is: $$$|\vec{u}|=\sqrt{u_1^2+u_2^2}$$$
If $$\vec{u}=(3,4)$$ then its magnitude is: $$|\vec{u}|=\sqrt{3^2+4^2}=\sqrt{25}=5$$.
2) Using the coordinates of the origin and the ending points. If $$A=(x_1,y_1)$$ and $$B=(x_2,y_2)$$, then: $$$ |\overrightarrow{AB}|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$$
If $$A=(-2,3)$$ and $$B=(2,0)$$, the magnitude of $$\overrightarrow{AB}$$, is:
$$$ |\overrightarrow{AB}|=\sqrt{(2-(-2))^2+(0-3)^2}=\sqrt{4^2+3^2}=\sqrt{25}=5$$$
