Conceptes fonamentals dels vectors

Un vector fix $\vec{A B}$ és un segment orientat que queda determinat per l'origen $A$ i l'extrem $B$ .

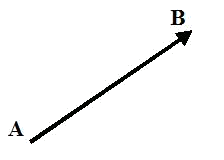
imagen

Les característiques principals d'un vector fix $\vec{A B}$ són les següents:

Direcció d'un vector fix $\vec{A B}$ : És la determinada per la recta que conté $\vec{A B}$ i totes les seves paral·leles.
Sentit d'un vector fix $\vec{A B}$ : És el que va de l'origen a l'extrem (determinat per la punta de la fletxa).
Mòdul d'un vector fix $\vec{A B}$ : És la longitud del segment $A B$ . Es representa per $| \vec{A B} |$ i sempre és un nombre positiu o zero.

Per exemple, un carrer té sentit prohibit, no direcció prohibida. O bé, en un mateix carrer poden haver dos sentits, però sempre tindrà una única direcció.

Classes de vectors

Dos vectors són equipol·lents quan tenen igual mòdul, direcció i sentit.

Exemple

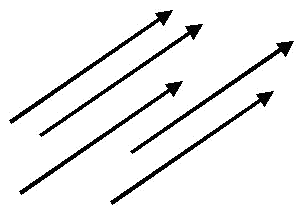
Els vectors representats en la següent imatge són equipol·lents. imagen

El conjunt de tots els vectors equipol·lents a un vector donat $\vec{A B}$ , s'anomena vector lliure. És a dir els vectors lliures tenen el mateix mòdul, direcció i sentit.

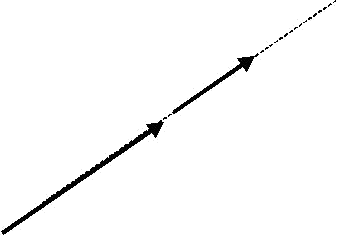
Els vectors lligats són vectors equipol·lents que actuen en la mateixa recta. És a dir, són els vectors fixos que tenen el mateix mòdul, direcció, sentit i es troben en la mateixa recta.

imagen

Els vectors oposats tenen el mateix mòdul, direcció, i diferent sentit.

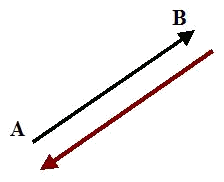
imagen

Exemple

$\vec{u}$ i $- \vec{u}$ són vectors oposats ja que tenen el mateix mòdul i direcció, en canvi el seu sentit és el contrari.

Els vectors unitaris són aquells tals que el seu mòdul és $1$ , és a dir, $| \vec{u} | = 1$ .

Com determinar un vector

Coneixent les coordenades de l'origen $A$ , i de l'extrem $B$ , podem determinar les components del vector $\vec{A B}$ que formen $A$ i $B$ , restant a les coordenades de l'extrem les de l'origen: $\vec{A B} = (x_{2}, y_{2}) - (x_{1}, y_{1}) = (x_{2} - x_{1}, y_{2} - y_{1})$ On, $A$ és el punt $(x_{1}, y_{1})$ i $B$ el punt $(x_{2}, y_{2})$ .

Exemple

Si $A = (3, - 1)$ i $B = (5, 2)$ , les components del vector $\vec{A B}$ són: $(5, 2) - (3, - 1) = (5 - 3, 2 - (- 1)) = (2, 3)$ .

Recordem que en aquest cas $A$ és l'origen i $B$ és l'extrem del vector $\vec{A B}$ .

Com calcular el mòdul d'un vector

1) A partir dels seus components. Si tenim el vector $\vec{u} = (u_{1}, u_{2})$ , el mòdul de $\vec{u}$ és: $| \vec{u} | = \sqrt{u_{1}^{2} + u_{2}^{2}}$

Exemple

Si $\vec{u} = (3, 4)$ el seu mòdul és: $| \vec{u} | = \sqrt{3^{2} + 4^{2}} = \sqrt{25} = 5$ .

2) A partir de les coordenades dels punts. Si $A = (x_{1}, y_{1})$ i $B = (x_{2}, y_{2})$ , aleshores: $| \vec{A B} | = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}$

Exemple

Si $A = (- 2, 3)$ i $B = (2, 0)$ , el mòdul de $\vec{A B}$ , és:

$| \vec{A B} | = \sqrt{(2 - (- 2))^{2} + (0 - 3)^{2}} = \sqrt{4^{2} + 3^{2}} = \sqrt{25} = 5$