Un vector fijo $$\overrightarrow{AB}$$ es un segmento orientado que queda determinado por el origen $$A$$ y el extremo $$B$$.
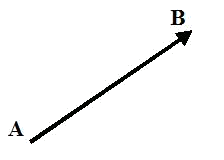
as características principales de un vector fijo $$\overrightarrow{AB}$$ son las siguientes:
- Dirección de un vector fijo $$\overrightarrow{AB}$$: es la determinada por la recta que contiene $$\overrightarrow{AB}$$ y todas sus paralelas.
- Sentido de un vector fijo $$\overrightarrow{AB}$$: es el que va del origen al extremo (determinado por la punta de la flecha).
- Módulo de un vector fijo $$\overrightarrow{AB}$$: es la longitud del segmento $$AB$$. Se representa por $$|\overrightarrow{AB}|$$ y siempre es un número positivo o zero.
Por ejemplo, una calle tiene sentido prohibido, no dirección prohibida. O bien, en una misma calle pueden haber dos sentidos, pero siempre tendrá una única dirección.
Clases de vectores
Dos vectores son equipolentes cuando tienen igual módulo, dirección y sentido.
Los vectores representados en la siguiente imagen son equipolentes.
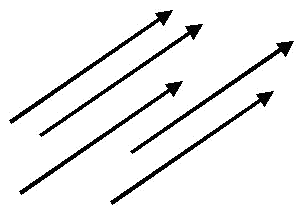
El conjunto de todos los vectores equipolentes a un vector dado $$\overrightarrow{AB}$$, se llama vector libre. Es decir los vectores libres tienen el mismo módulo, dirección y sentido.
Los vectores ligados son vectores equipolentes que actúan en la misma recta. Es decir, son los vectores fijos que tienen el mismo módulo, dirección, sentido y se encuentran en la misma recta.
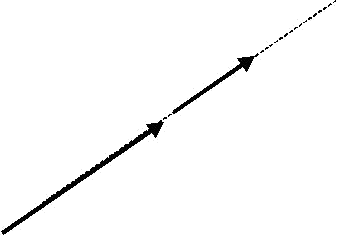
Los vectores opuestos tienen el mismo módulo, dirección, y distinto sentido.
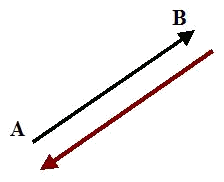
$$\vec{u}$$ y $$-\vec{u}$$ son vectores opuestos dado que tienen el mismo módulo y dirección, en cambio su sentido es el contrario.
Los vectores unitarios son aquellos en que su módulo es $$1$$, es decir, $$|\vec{u}|=1$$.
Cómo determinar un vector
Conociendo las coordenadas del origen $$A$$, y del extremo $$B$$, podemos determinar las componentes del vector $$\overrightarrow{AB}$$ que forman $$A$$ y $$B$$, restando a las coordenadas del extremo las del origen: $$$ \overrightarrow{AB}= (x_2,y_2)-(x_1,y_1)=(x_2-x_1, y_2-y_1)$$$ Donde $$A$$ es el punto $$(x_1,y_1)$$ y $$B$$ el punto $$(x_2,y_2)$$.
Si $$A=(3, -1)$$ y $$B=(5,2)$$, las componentes del vector $$\overrightarrow{AB}$$ son: $$(5,2)-(3,-1)=(5-3,2-(-1))=(2,3)$$.
Recordamos que en este caso $$A$$ es el origen y $$B$$ es el extremo del vector $$\overrightarrow{AB}$$.
Cómo calcular el módulo de un vector
1) A partir de sus componentes. Si tenemos el vector $$\vec{u}=(u_1,u_2)$$, el módulo de $$\vec{u}$$ es: $$$|\vec{u}|=\sqrt{u_1^2+u_2^2}$$$
Si $$\vec{u}=(3,4)$$ su módulo es: $$|\vec{u}|=\sqrt{3^2+4^2}=\sqrt{25}=5$$.
2) A partir de las coordenadas de los puntos. Si $$A=(x_1,y_1)$$ y $$B=(x_2,y_2)$$, entonces: $$$ |\overrightarrow{AB}|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$$
Si $$A=(-2,3)$$ y $$B=(2,0)$$, el módulo de $$\overrightarrow{AB}$$, es:
$$$ |\overrightarrow{AB}|=\sqrt{(2-(-2))^2+(0-3)^2}=\sqrt{4^2+3^2}=\sqrt{25}=5$$$
