Law of sines and cosines

Both the law of sines and the law of cosines are applicable to any kind of triangles, as opposed to the Pythagoras theorem that only applies to right-angled triangles.

Law of sines

The law of sines is a proportionality relation between the lengths of the sides of a triangle and the sines of the opposite angles. Given the triangle:

imagen

We have: $\frac{a}{\sin α} = \frac{b}{\sin β} = \frac{c}{\sin γ}$

Example

Knowing that two angles of a triangle are: $A = 30^{\circ}$ , $B = 45^{\circ}$ and that the side opposite to the angle $B$ is $b = \sqrt{2}$ cm, we can calculate the side $a$ opposite to the angle $A$ by means of the law of sines. Let's see how:

First, we need to identify the information given in the problem. We have the following triangle:

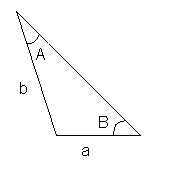
imagen

We know two angles and one side of this triangle. For one of the angles that we know, $B$ , we also know the length of the opposite side, $b$ . And the side we are looking for is the opposite to the other known angle, $A$ . Therefore, in the equality of the law of sines $\frac{a}{\sin A} = \frac{b}{\sin B}$

we only have one unknown. The rest is information given in the problem. And so, we can compute: $a = \frac{b \cdot \sin A}{\sin B} = \frac{\sqrt{2} \cdot \sin 30}{\sin 45} = \frac{\sqrt{2} \frac{1}{2}}{\frac{\sqrt{2}}{2}} = \frac{2 \sqrt{2}}{2 \sqrt{2}} = 1$

Law of cosines

The law of cosines can be understood like a generalization of Pythagoras theorem for any kind of triangle. In other words, if we apply the law of cosines to a right triangle we obtain the same result as in Pythagoras theorem. We will get a relationship between the length of one side and the length of the other two and with the cosine of the angle formed by them. Given the triangle,

imagen

We have: $a^{2} = b^{2} + c^{2} - 2 \cdot b \cdot c \cdot \cos α$ This can be applied to any of the sides, so we also have these two identities: $\begin{array}{rc} b^{2} & = & a^{2} + c^{2} - 2 \cdot a \cdot c \cdot \cos β \\ c^{2} & = & a^{2} + b^{2} - 2 \cdot a \cdot b \cdot \cos γ \end{array}$

Example

Let's suppose that we know three sides of a triangle, $a = 2, b = 3, c = \sqrt{7}$ and we want to know the angles. From the law of cosines we know: $c^{2} = a^{2} + b^{2} - 2 \cdot a \cdot b \cdot \cos γ \Rightarrow 7 = 4 + 9 - 2 \cdot 2 \cdot 3 \cdot \cos γ \Rightarrow$ $6 = 12 \cdot \cos γ \Rightarrow \cos γ = \frac{1}{2} \Rightarrow γ = 60$

Applying the law of cosines again we can find the second angle: $b^{2} = a^{2} + c^{2} - 2 \cdot a \cdot c \cdot \cos β \Rightarrow 9 = 4 + 7 - 2 \cdot 2 \cdot \sqrt{7} \cdot \cos β \Rightarrow$ $a = 4 \sqrt{7} \cdot \cos β \Rightarrow \cos β = \frac{1}{2} \sqrt{7} \Rightarrow β = {79.10}^{\circ}$

Finally, using our knowledge that the sum of the angles of a triangle is $180^{\circ}$ , we have $α = 180 - β - γ = {40.9}^{\circ}$