Tant el teorema del sinus com el del cosinus són resultats que es poden aplicar a qualsevol triangle, és a dir, no ens cal que el triangle sigui rectangle, com ens passava amb el teorema de Pitàgores.
Teorema del sinus
El teorema del sinus és una relació de proporcionalitat entre les longituds dels costats d'un triangle i el sinus dels rectangles relativament oposats. Donat el triangle:
Es té: $$$\displaystyle \frac{a}{\sin \alpha}=\frac{b}{\sin \beta}=\frac{c}{\sin \gamma}$$$
Sabent que dos angles d'un triangle són: $$A=30^\circ$$, $$B=45^\circ$$ i que el costat oposat a l'angle $$B$$ mesura $$b=\sqrt{2}$$ cm, podem calcular el costat $$a$$, l'oposat a l'angle $$A$$, a partir del teorema del sinus. Anem a veure com:
Identificant les dades del problema, tenim el següent triangle:
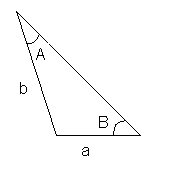
D'aquest triangle coneixem dos angles i un costat. Un dels angles que coneixem, $$B$$, té com a costat oposat un costat conegut, $$b$$. I el costat que estem buscant té com a angle oposat l'altre angle conegut, $$A$$.
Per tant, en la igualtat que ens proporciona el teorema del sinus: $$$\displaystyle \frac{a}{\sin A}=\frac{b}{\sin B}$$$
Només tenim una incògnita, la resta són dades del problema. Així doncs, aïllant a obtenim: $$$\displaystyle a=\frac{b \cdot \sin A}{\sin B}=\frac{\sqrt{2} \cdot \sin 30}{\sin 45}=\frac{\sqrt{2}\frac{1}{2}}{\frac{\sqrt{2}}{2}}=\frac{2\sqrt{2}}{2\sqrt{2}}=1$$$
Teorema del cosinus
El teorema del cosinus es pot entendre com una generalització del teorema de Pitàgores per triangles qualssevol, és a dir, si apliquem el teorema del cosinus en un triangle rectangle obtenim el mateix resultat que el teorema de Pitàgores. Ens relaciona la longitud d'un costat amb les longituds dels altres i amb el cosinus de l'angle format per aquests. Donat el triangle,
Es té: $$$a^2= b^2+c^2-2 \cdot b \cdot c \cdot \cos \alpha$$$ A més no privilegia cap banda, de manera que, realment, es tenen unes altres dues igualtats $$$\begin{array}{rc} b^2&=&a^2+c^2-2\cdot a \cdot c \cdot \cos \beta \\ c^2 &=& a^2+b^2-2\cdot a \cdot b \cdot \cos \gamma \end{array}$$$
Suposem que d'un triangle coneixem els tres costats, $$a=2, b=3, c=\sqrt{7}$$ i volem conèixer els angles.
Pel teorema del cosinus sabem: $$$c^2=a^2+b^2-2\cdot a \cdot b \cdot \cos \gamma \Rightarrow 7=4+9-2\cdot 2 \cdot 3\cdot \cos \gamma \Rightarrow $$$ $$$6= 12 \cdot \cos \gamma \Rightarrow \cos \gamma= \displaystyle \frac{1}{2} \Rightarrow \gamma =60 $$$
Aplicant altre cop el teorema del cosinus podem trobar un segon angle: $$$b^2=a^2+c^2-2 \cdot a \cdot c \cdot \cos \beta \Rightarrow 9=4+7-2\cdot 2 \cdot \sqrt{7} \cdot \cos \beta \Rightarrow $$$ $$$a=4\sqrt{7}\cdot \cos \beta \Rightarrow \cos \beta=\displaystyle \frac{1}{2}\sqrt{7} \Rightarrow \beta=79.10^\circ$$$
Finalment, utilitzant que la suma dels rectangles d'un triangle és $$180^\circ$$, tenim $$$\alpha=180-\beta-\gamma=40.9^\circ$$$