Teorema del seno y del coseno

Tanto el teorema del seno como el del coseno son resultados que se pueden aplicar a cualquier triángulo, es decir, no nos hace falta que el triángulo sea rectángulo, como nos pasaba con el teorema de Pitágoras.

Teorema del seno

El teorema del seno es una relación de proporcionalidad entre las longitudes de los lados de un triángulo y los senos de los ángulos relativamente opuestos. Dado el triángulo:

Imagen

Se tiene: $\frac{a}{\sin α} = \frac{b}{\sin β} = \frac{c}{\sin γ}$

Ejemplo

Sabiendo que dos ángulos de un triángulo son: $A = 30^{\circ}$ , $B = 45^{\circ}$ y que el lado relativamente opuesto al ángulo $B$ mide $b = \sqrt{2}$ cm, podemos calcular el lado $a$ , el relativamente opuesto al ángulo $A$ , a partir del teorema del seno. Vamos a ver cómo:

Identificando los datos del problema, tenemos el siguiente triángulo:

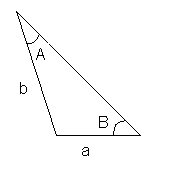
Imagen

De este triángulo conocemos dos ángulos y un lado. Uno de los ángulos que conocemos, $B$ , tiene como lado relativamente opuesto un lado conocido, $b$ . Y el lado que estamos buscando tiene como ángulo relativamente opuesto el otro ángulo conocido, $A$ . Por lo tanto, en la igualdad que nos proporciona el teorema del seno:

$\frac{a}{\sin A} = \frac{b}{\sin B}$

Sólo tenemos una incógnita, lo demás son datos del problema. Así pues, despejando a obtenemos: $a = \frac{b \cdot \sin A}{\sin B} = \frac{\sqrt{2} \cdot \sin 30}{\sin 45} = \frac{\sqrt{2} \frac{1}{2}}{\frac{\sqrt{2}}{2}} = \frac{2 \sqrt{2}}{2 \sqrt{2}} = 1$

Teorema del coseno

El teorema del coseno se puede entender como una generalización del teorema de Pitágoras para triángulos cualesquiera, es decir, si aplicamos el teorema del coseno en un triángulo rectángulo obtenemos el mismo resultado que el teorema de Pitágoras. Nos relaciona la longitud de un lado con las longitudes de los otros y con el coseno del ángulo formado por éstos. Dado el triángulo,

Imagen

Se tiene: $a^{2} = b^{2} + c^{2} - 2 \cdot b \cdot c \cdot \cos α$ Además no privilegia ningún lado, de manera que, realmente, se tienen otras dos igualdades $\begin{array}{rc} b^{2} & = & a^{2} + c^{2} - 2 \cdot a \cdot c \cdot \cos β \\ c^{2} & = & a^{2} + b^{2} - 2 \cdot a \cdot b \cdot \cos γ \end{array}$

Ejemplo

Supongamos que de un triángulo conocemos los tres lados, $a = 2, b = 3, c = \sqrt{7}$ y queremos conocer los ángulos.

Por el teorema del coseno sabemos: $c^{2} = a^{2} + b^{2} - 2 \cdot a \cdot b \cdot \cos γ \Rightarrow 7 = 4 + 9 - 2 \cdot 2 \cdot 3 \cdot \cos γ \Rightarrow$ $6 = 12 \cdot \cos γ \Rightarrow \cos γ = \frac{1}{2} \Rightarrow γ = 60$

Aplicando otra vez el teorema del coseno podemos encontrar un segundo ángulo: $b^{2} = a^{2} + c^{2} - 2 \cdot a \cdot c \cdot \cos β \Rightarrow 9 = 4 + 7 - 2 \cdot 2 \cdot \sqrt{7} \cdot \cos β \Rightarrow$ $a = 4 \sqrt{7} \cdot \cos β \Rightarrow \cos β = \frac{1}{2} \sqrt{7} \Rightarrow β = {79.10}^{\circ}$

Finalmente, utilizando que la suma de los ángulos de un triángulo es $180^{\circ}$ , tenemos $α = 180 - β - γ = {40.9}^{\circ}$