Funciones trigonométricas: características de seno, coseno y tangente

La función seno, $sin(x)$

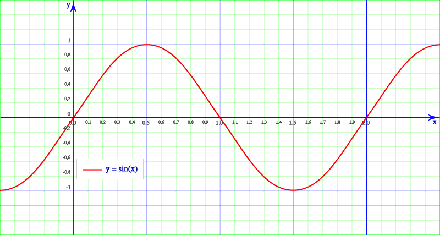
1. Dominio: $\mathbb{R}$
2. Imagen: $[-1,1]$
3. Periodo: $2\pi$ rad
4. Continuidad: Continua en todo $\mathbb{R}$
5. Creciente en: $\dots \bigcup ({\displaystyle -\frac{\pi }{2},\frac{\pi }{2})\bigcup ({\displaystyle \frac{3\pi }{2},\frac{5\pi }{2})\bigcup \dots }}$
6. Decreciente en: $\dots \bigcup ({\displaystyle \frac{\pi }{2},\frac{3\pi }{2})\bigcup ({\displaystyle \frac{5\pi }{2},\frac{7\pi }{2})\bigcup \dots }}$
7. Máximos en: $\{{\displaystyle \frac{\pi }{2}+2\pi \cdot k}$, $k\in \mathbb{Z}\}$
8. Mínimos en: $\{{\displaystyle \frac{3\pi }{2}+2\pi \cdot k}$, $k\in \mathbb{Z}\}$
9. Paridad: Impar, $\sin x=-\sin (-x)$
10. Cortes con el eje Ox: $x=k\cdot \pi$, $k\in \mathbb{Z}$

La función coseno, $cos(x)$

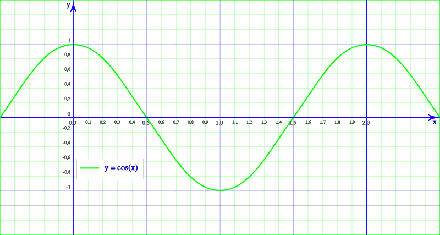
1. Dominio: $\mathbb{R}$
2. Imagen: $[-1,1]$
3. Periodo: $2\pi$ rad
4. Continuidad: Continua en todo $\mathbb{R}$
5. Creciente en: $\dots \bigcup (-\pi ,0)\bigcup (\pi ,2\pi )\bigcup \dots$
6. Decreciente en: $\dots \bigcup (0,\pi )\bigcup (2\pi ,3\pi )\bigcup \dots$
7. Máximos en: $\{2\pi \cdot k$, $k\in \mathbb{Z}\}$
8. Mínimos en: $\{\pi \cdot (2k+1)$, $k\in \mathbb{Z}\}$
9. Paridad: Par $\cos x=\cos (-x)$
10. Cortes con el eje Ox: $x={\displaystyle \frac{\pi }{2}+k\cdot \pi }$, $k\in \mathbb{Z}$

La función tangente, $tan(x)$

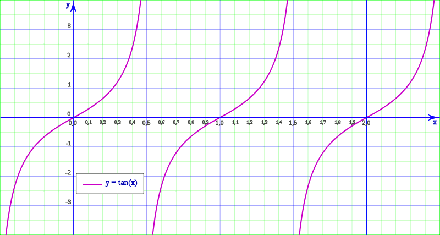
1. Dominio: $\mathbb{R}-\{(2k+1)\cdot {\displaystyle \frac{\pi }{2},k\in \mathbb{Z}\}=\mathbb{R}-\{\dots ,{\displaystyle -\frac{\pi }{2},\frac{\pi }{2},\frac{3\pi }{2},\dots \}}}$
2. Imagen: $\mathbb{R}$
3. Periodo: $\pi$ rad
4. Continuidad: Continua en $\mathbb{R}-\{{\displaystyle \frac{\pi }{2}+k\pi ,k\in \mathbb{Z}\}}$
5. Creciente en: $\mathbb{R}$
6. Máximos: no tiene
7. Mínimos: no tiene
8. Paridad: Impar $\tan x=-\tan (-x)$
9. Cortes con el eje Ox: $x=k\cdot \pi ,k\in \mathbb{Z}$