Funcions trigonomètriques: característiques de sinus, cosinus i tangent

La funció sinus, $sin(x)$

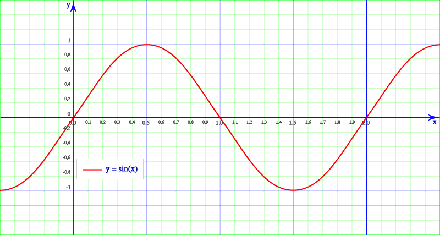
1. Domini: $\mathbb{R}$
2. Imatge: $[-1,1]$
3. Període: $2\pi$ rad
4. Continuïtat: Contínua en tot $\mathbb{R}$
5. Creixent en: $\dots \cup ({\displaystyle -\frac{\pi }{2},\frac{\pi }{2})\cup ({\displaystyle \frac{3\pi }{2},\frac{5\pi }{2})\cup \dots }}$
6. Decreixent en: $\dots \cup ({\displaystyle \frac{\pi }{2},\frac{3\pi }{2})\cup ({\displaystyle \frac{5\pi }{2},\frac{7\pi }{2})\cup \dots }}$
7. Màxims en: $\{{\displaystyle \frac{\pi }{2}+2\pi \cdot k}$, $k\in \mathbb{Z}\}$
8. Mínims en: $\{{\displaystyle \frac{3\pi }{2}+2\pi \cdot k}$, $k\in \mathbb{Z}\}$
9. Paritat: Senar, $\sin x=-\sin (-x)$
10. Talls amb l'eix Ox: $x=k\cdot \pi$, $k\in \mathbb{Z}$

La funció cosinus, $cos(x)$

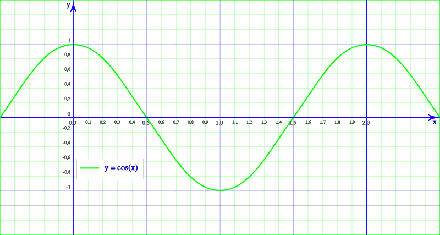
1. Domini: $\mathbb{R}$
2. Imatge: $[-1,1]$
3. Període: $2\pi$ rad
4. Continuïtat: Contínua en tot $\mathbb{R}$
5. Creixent en: $\dots \cup (-\pi ,0)\cup (\pi ,2\pi )\cup \dots$
6. Decreixent en: $\dots \cup (0,\pi )\cup (2\pi ,3\pi )\cup \dots$
7. Màxims en: $\{2\pi \cdot k$, $k\in \mathbb{Z}\}$
8. Mínims en: $\{\pi \cdot (2k+1)$, $k\in \mathbb{Z}\}$
9. Paritat: Parella $\cos x=\cos (-x)$
10. Talls amb l'eix Ox: $x={\displaystyle \frac{\pi }{2}+k\cdot \pi }$, $k\in \mathbb{Z}$

La función tangent, $tan(x)$

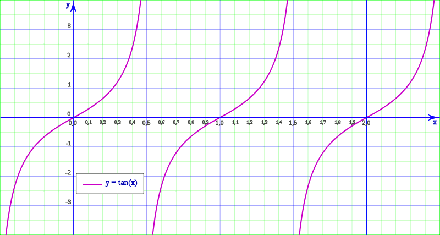
1. Domini: $\mathbb{R}-\{(2k+1)\cdot {\displaystyle \frac{\pi }{2},k\in \mathbb{Z}\}=\mathbb{R}-\{\dots ,{\displaystyle -\frac{\pi }{2},\frac{\pi }{2},\frac{3\pi }{2},\dots \}}}$
2. Imatge: $\mathbb{R}$
3. Període: $\pi$ rad
4. Continuïtat: Contínua en $\mathbb{R}-\{{\displaystyle \frac{\pi }{2}+k\pi ,k\in \mathbb{Z}\}}$
5. Creixent en: $\mathbb{R}$
6. Màxims: no en té
7. Mínims: no en té
8. Paritat: Senar $\tan x=-\tan (-x)$
9. Talls amb l'eix Ox: $x=k\cdot \pi ,k\in \mathbb{Z}$